某学校100名学生期中考试语文成绩的频率分布直方图如下右图所示,其中成绩分组区间是: ,
, ,
, ,
,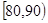 ,
,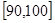 。
。
求图中a的值;
根据频率分布直方图,估计这100名学生语文成绩的平均分;
若这100名学生语文成绩某些分数段的人数 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数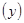
之比如下表所示,求数学成绩在 之外的人数。
之外的人数。
| 分数段 |
 |
 |
 |
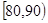 |
x :y :y |
1:1 |
2:1 |
3:4 |
4:5 |
相关知识点
推荐套卷
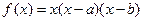 。
。 ,函数
,函数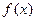 在
在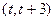 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求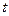 的取值范围;
的取值范围;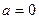 时,
时,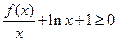 对任意的
对任意的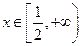 恒成立,求
恒成立,求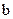 的取值范围;
的取值范围; :直线
:直线 与抛物线
与抛物线 至少有一个公共点;命题
至少有一个公共点;命题 :函数
:函数 在
在 上单调递减。若“
上单调递减。若“ ”为假,“
”为假,“ ”为真,求实数
”为真,求实数 的取值范围。
的取值范围。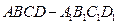 是正方体,其中
是正方体,其中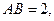
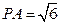
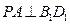 ;
;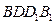 所成的锐二面角
所成的锐二面角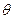 的余弦值;
的余弦值;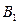 到平面PAD的距离
到平面PAD的距离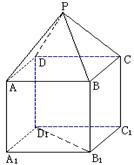
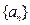 的前
的前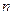 项和为
项和为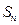 ,且
,且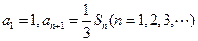 ,试求:
,试求: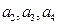 的值;
的值;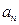 ;
;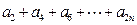 的值。
的值。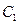 中心在原点,焦点坐标是
中心在原点,焦点坐标是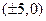 ,并且双曲线的离心率为
,并且双曲线的离心率为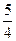 。
。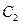 以双曲线
以双曲线 粤公网安备 44130202000953号
粤公网安备 44130202000953号