高中数学误差估计试题

甲乙两名运动员在某项测试中的8次成绩如茎叶图所示，，分别表示甲乙两名运动员这项测试成绩的平均数，，分别表示甲乙两名运动员这项测试成绩的标准差，则有（   ）

A．	B．
C．	D．

（本小题满分13分）某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分别随机抽取100个，整理得到数据分组及频率分布表和频率分布直方图： 

分组（日销售量）	频率（甲种酸奶）
[ 0，10]	0．10
（10，20]	0．20
（20，30]	0．30
（30，40]	0．25
（40，50]	0．15

 

（Ⅰ）写出频率分布直方图中的的值，并作出甲种酸奶日销售量的频率分布直方图；

（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为，，试比较与的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替,试估计乙种酸奶在未来一个月（按30天计算）的销售总量．

某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图，则乙同学这5次数学成绩的中位数是         ；已知两位同学这5次成绩的平均数都是84，成绩比较稳定的是             （第二个空填“甲”或“乙”）．

某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为,若低于60分的人数是15人,则该班的学生人数是（    ）

A．

B．

C．

D．

若某市所中学参加中学生合唱比赛的得分用茎叶图表示（如图），其中茎为十位数，叶为个位数，则这组数据的中位数是（  ）

A．

B．

C．

D．

若从总体中随机抽取的样本为，则该总体的标准差的点估计值是        ．

（本小题满分12分）我市为积极相应《全民健身条例》大力开展学生体育活动，如图是委托
调查机构在市区的两所学校校、校中分别随机抽取了名高二年级的学生当月体育锻炼时间的茎
叶图（单位：小时）

（1）根据茎叶图，分别写将两所学校学生当月体育锻炼 时间的众数、中位数和平均数填入下表；

	校	校
众数
中位数
平均数

 
（2）根据茎叶图，求校学生的月体育锻炼时间的方差；
（3）若学生月体育锻炼的时间低于小时，就说明该生体育锻炼时间严重不足．根据茎叶图估计、
两所学校的学生体育锻炼严重不足的频率．

（本小题满分12分）在科普知识竞赛前的培训活动中，将甲、乙两名学生的6次培训成绩（百分制）制成如图所示的茎叶图：
   
（Ⅰ）若从甲、乙两名学生中选择1人参加该知识竞赛，你会选哪位？请运用统计学的知识说明理由；
（Ⅱ）若从学生甲的6次培训成绩中随机选择2个，记选到的分数超过87分的个数为，求的分布列和数学期望．

在一次考试中，5名同学数学、物理成绩如下表所示：

学生	A	B	C	D	E
数学（x分）	89	91	93	95	97
物理（y分）	87	89	89	92	93

 
（1）根据表中数据，求物理分对数学分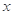的回归方程：
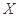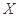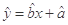（2）要从4名数学成绩在90分以上的同学中选出2名参加一项活动，以表示选中的同学中物理成绩高于90分的人数，求随机变量的分布列及数学期望．（附：回归方程中，，）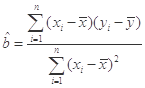

（本小题满分12分）某中学在高二年级开设大学先修课程《线性代数》，共有50名同学选修，其中男同学30名，女同学20名.为了对这门课程的教学效果进行评估，学校按性别采用分层抽样的方法抽取5人进行考核.
（1）求抽取的5人中男、女同学的人数；
（2）考核前，评估小组打算从抽取的5人中随机选出2名同学进行访谈，求选出的两名同学中恰有一名女同学的概率.

（原创）某学校高三某班某个学习小组8名同学在上期末考试中物理成绩如下面茎叶图所示，则该小组物理成绩平均值与中位数之和为              ．

（本小题满分12分）根据我国发布了新修订的《环境空气质量标准》指出空气质量指数在为优秀，人类可正常活动．某市环保局对该市2014年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为，， ， ，由此得到样本的空气质量指数频率分布直方图．

（Ⅰ）若空气质量指数大于或等于15且小于35认为是良好的，求该市在这次监测中空气质量
为良好的天数，并根据频率分布直方图估计这一年度的空气质量指数的平均值；
（Ⅱ）如果空气质量指数不超过15，就认定空气质量为“优”，则从这一年的监测数据中随机
抽取3天的数值，其中达到“优”的天数为，求的分布列和数学期望．

若样本的方差是2，则样本的方差是           ．

某校高二文科班从甲、乙两个班各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的平均分是85，乙班学生成绩的中位数是83，则的值为_______________．

（本小题满分12分）某市规定，高中学生三年在校期间参加不少于小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段，，，，（单位：小时）进行统计，其频率分布直方图如图所示．

（1）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；
（2）从全市高中学生（人数很多）中任意选取3位学生，记为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量的分布列和数学期望.