(本小题满分13分)
如图,⊙O在平面 内,AB是⊙O的直径,
内,AB是⊙O的直径, 平面
平面 ,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求证: 平面
平面 .
.
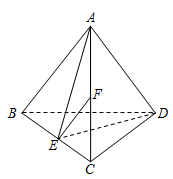
(本小题满分14分)如图,在四面体 中,
中, ,点
,点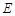 是
是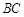 的中点,点
的中点,点 在线段
在线段 上,且
上,且 .
.
(1)若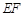 ∥平面
∥平面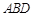 ,求实数
,求实数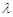 的值;
的值;
(2)求证:平面 平面
平面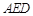 .
.
已知直线 与平面
与平面 ,则下列四个命题中假命题是
,则下列四个命题中假命题是
A.如果 ,那么 ,那么 |
B.如果 ,那么 ,那么 |
C.如果 ,那么 ,那么 |
D.如果 ,那么 ,那么 |
三棱锥 中,
中, ,
,  ,D为AB的中点, ∠ABC=90°,则点D到面SBC的距离等于_____________.
,D为AB的中点, ∠ABC=90°,则点D到面SBC的距离等于_____________.
如图,在底面为平行四边形的四棱锥 中,
中,  ,
, 平面
平面 ,点
,点 是
是 的中点.
的中点.
(1)求证: ;
;
(2)求证: 平面
平面 ;
;
(本小题满分14分)如图,在三棱柱 中,各个侧面均是边长为
中,各个侧面均是边长为 的正方形,
的正方形, 为线段
为线段 的中点.
的中点.
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)求证:直线 ∥平面
∥平面 ;
;
(Ⅲ)设 为线段
为线段 上任意一点,在
上任意一点,在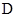
 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点 ,使
,使
 ,并说明理由.
,并说明理由.
正四面体P-ABC中,D、E、F分别是棱AB、BC、CA的中点,下列结论中不成立的是( )
A.BC∥面PDF
B.DF⊥面PAE
C.面PDF⊥面PAE
D.面PDF⊥面ABC
如图,正方形ABCD中,E,F分别是BC,CD的中点,H是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合于G点,则在四面体A-EFG中必有( )
A.AG 平面EFG 平面EFG |
B.AH 平面EFG 平面EFG |
C.GF 平面AEF 平面AEF |
D.GH 平面AEF 平面AEF |
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( ).
| A.若α⊥β,m⊂α,n⊂β,则m⊥n |
| B.若α∥β,m⊂α,n⊂β,,则m∥n |
| C.若m⊥n,m⊂α,n⊂β,则α⊥β |
| D.若m⊥α,m∥n,n∥β,则α⊥β |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列命题为真命题的是( )
是两个不同的平面,则下列命题为真命题的是( )
A.若 |
B.若 |
C.若 |
D.若 |
已知直线l∥平面α,直线m Ìα,则直线l和m的位置关系是 .
(平行、相交、异面三种位置关系中选)
如图,在正四棱锥 中,
中, ,
, ,
, 分别是
分别是 ,
, ,
, 的中点,动点
的中点,动点 在线段
在线段 上运动时,下列四个结论:①
上运动时,下列四个结论:① ;②
;② ;③
;③ ;④
;④ .中恒成立的为( )
.中恒成立的为( )
| A.①③ | B.③④ | C.①② | D.②③④ |