四棱锥P-ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC=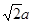 ,
,
(1)求证:PD⊥平面ABCD;
(2)求证,直线PB与AC垂直;
若 、
、 、
、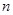 是互不相同的空间直线,α、β是不重合的平面,则下列结论正确的是
是互不相同的空间直线,α、β是不重合的平面,则下列结论正确的是
A.   |
B.   |
C.   |
D.   |
设 是空间三条直线,
是空间三条直线, 是空间两个平面,则下列命题中,逆命题不正确的是( )
是空间两个平面,则下列命题中,逆命题不正确的是( )
A.当 时,若 时,若 ,则 ,则 |
B.当 且 且 是 是 在 在 内的射影时,若 内的射影时,若 ,则 ,则 |
C.当 时,若 时,若 ,则 ,则 |
D.当 且 且 时,若 时,若 ,则 ,则 |
已知 为两条不同的直线,
为两条不同的直线, 为两个不同的平面,且
为两个不同的平面,且 ,给出下列结论:
,给出下列结论:
①若 ∥
∥ ,则
,则 ∥
∥ ;
;
②若 ∥
∥ ,则
,则 ∥
∥ ;
;
③若 ⊥
⊥ ,则
,则 ⊥
⊥ ;
;
④若 ⊥
⊥ ,则
,则 ⊥
⊥
其中正确结论的个数是()
| A.0 | B.1 | C.2 | D.3 |
已知 为两条不同的直线,
为两条不同的直线, 为两个不同的平面,且
为两个不同的平面,且 ,给出下列结论:①若
,给出下列结论:①若 ∥
∥ ,则
,则 ∥
∥ ;②若
;②若 ∥
∥ ,则
,则 ∥
∥ ;③若
;③若 ⊥
⊥ ,则
,则 ⊥
⊥ ; ④若
; ④若 ⊥
⊥ ,则
,则 ⊥
⊥ ;其中正确结论的个数是( )
;其中正确结论的个数是( )
| A.0 | B.1 | C.2 | D.3 |
如图,ABCD-A1B1C1D1为正方体,下面结论错误的是().
| A.BD∥平面CB1D1 |
| B.AC1⊥BD |
| C.AC1⊥平面CB1D1 |
| D.异面直线AD与CB1角为60° |
下列四个命题中错误的是()
A.若直线 、 、 互相平行,则直线 互相平行,则直线 、 、 确定一个平面 确定一个平面 |
| B.若四点不共面,则这四点中任意三点都不共线 |
| C.若两条直线没有公共点,则这两条直线是异面直线 |
| D.两条异面直线不可能垂直于同一个平面 |
如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
已知两个平面垂直,下列命题中:
(1)一个平面内已知直线必垂直于另一个平面内的任意一条直线;
(2)一个平面内已知直线必垂直于另一个平面内的无数条直线;
(3)一个平面内的任意一条直线必垂直于另一个平面;
(4)过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.其中正确命题的个数有
| A.1 | B.2 | C.3 | D.4 |
下列命题中, 表示两条不同的直线,
表示两条不同的直线, 表示三个不同的平面:
表示三个不同的平面:
① 若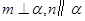 则
则 ;
;
② 若 ,则
,则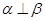 ;
;
③ 若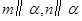 ,则
,则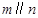 ;
;
④ 若 ,则
,则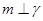
正确的命题是()
| A.①③ | B.②③ | C.①④ | D.②④ |
在空间直角坐标系 中,点
中,点 到
到 平面的距离是()
平面的距离是()
A. |
B. |
C. |
D. |