在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面
ABCD,AE⊥BD,CB=CD=CF=1,
(1)求证:BD⊥平面AED;
(2)求B到平面FDC的距离.
已知 为两条不同的直线,
为两条不同的直线, 为两个不同的平面,且
为两个不同的平面,且 ,给出下列结论:①若
,给出下列结论:①若 ∥
∥ ,则
,则 ∥
∥ ;②若
;②若 ∥
∥ ,则
,则 ∥
∥ ;③若
;③若 ⊥
⊥ ,则
,则 ⊥
⊥ ; ④若
; ④若 ⊥
⊥ ,则
,则 ⊥
⊥ ;其中正确结论的个数是( )
;其中正确结论的个数是( )
| A.0 | B.1 | C.2 | D.3 |
设 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若 ,
, ,则
,则 ;
;
②若 ,
, ,
, ,
, ,则
,则 ;
;
③若 ,
, ,则
,则 ;
;
④若 ,
, ,
, ,
, ,则
,则
其中真命题的个数是 .
若m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中真命题是( )
| A.若m⊥β,m∥α,则α⊥β |
| B.若α∩γ=m,β∩γ=n,m∥n,则α∥β |
| C.若m⊂β,α⊥β,则m⊥α |
| D.若α⊥γ,α⊥β,则β⊥γ |
对于平面α和共面的直线m、n,下列命题正确的是( )
| A.若m、n与α所成的角相等,则m∥n |
| B.若m∥α,n∥α,则m∥n |
| C.若m⊥α,m⊥n,则n∥α |
D.若m α,n∥α,则m∥n α,n∥α,则m∥n |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列命题为真命题的是( )
是两个不同的平面,则下列命题为真命题的是( )
A.若 |
B.若 |
C.若 |
D.若 |
如图,三棱柱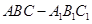 中,侧棱
中,侧棱 平面
平面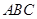 ,
,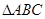 为等腰直角三角形,
为等腰直角三角形,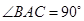 ,且
,且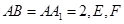 分别是
分别是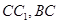 的中点.
的中点.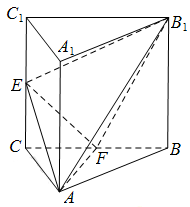
(1)求证: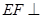 平面
平面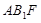 ;
;
(2)求锐二面角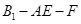 的余弦值;
的余弦值;
(3)若点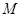 是
是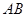 上一点,求
上一点,求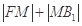 的最小值.
的最小值.
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点, D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF,正确的是( )

| A.(1)和(3) | B.(2)和(5) |
| C.(1)和(4) | D.(2)和(4) |
设 ,
, ,
, 是三个互不重合的平面,
是三个互不重合的平面, ,
, 是直线,给出下列命题:①
是直线,给出下列命题:① ,
, ,则
,则 ;②若
;②若 ,
, ,
, ,则
,则 ;③若
;③若 ,
, 在
在 内的射影互相垂直,则
内的射影互相垂直,则 ;④若
;④若 ,
, ,
, ,则
,则 ,其中正确命题的个数为( )
,其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
如图,三棱柱 中,侧棱
中,侧棱 底面
底面 ,底面三角形
,底面三角形 是正三角形,
是正三角形, 是
是 中点,则下列叙述正确的是
中点,则下列叙述正确的是
A. 与 与 是异面直线 是异面直线 |
B. 平面 平面 |
C. , , 为异面直线,且 为异面直线,且 |
D. 平面 平面 |
已知 为不同的直线,
为不同的直线, 为不同的平面,则下列说法正确的是
为不同的平面,则下列说法正确的是
A. |
B. |
C. |
D. |