四棱锥P-ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC=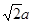 ,
,
(1)求证:PD⊥平面ABCD;
(2)求证,直线PB与AC垂直;
已知 为两条不同的直线,
为两条不同的直线,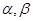 为两个不同的平面,给出下列4个命题:
为两个不同的平面,给出下列4个命题:
①若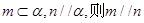
②若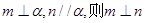
③若
④若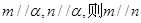
其中真命题的序号为( )
| A.①② | B.②③ | C.③④ | D.①④ |
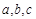 表示直线,
表示直线, 表示平面,下列命题正确的是( )
表示平面,下列命题正确的是( )
A.若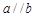 , ,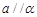 ,则 ,则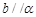 |
B.若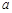 ⊥ ⊥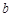 , , 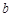 ⊥ ⊥ ,则 ,则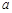 ⊥ ⊥ |
C.若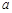 ⊥ ⊥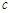 , ,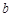 ⊥ ⊥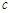 ,则 ,则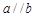 |
D.若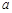 ⊥ ⊥ , ,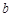 ⊥ ⊥ ,则 ,则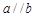 |
给岀四个命题:
(1)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(2)a,b为两个不同平面,直线a Ìa,直线b Ìa,且a∥b,b∥b , 则a∥b ;
(3)a,b为两个不同平面,直线m⊥a,m⊥b 则a∥b ;
(4)a,b为两个不同平面,直线m∥a,m∥b , 则a∥b .
其中正确的是( )
| A.(1) | B.(2) | C.(3) | D.(4) |
已知两个不同的平面α、β和两条不重合的直线,m、n,有下列四个命题:
①若m∥n,m⊥α,则n⊥α
②若m⊥α,m⊥β,则α∥β;
③若m⊥α,m∥n,n⊂β,则α⊥β;
④若m∥α,α∩β=n,则m∥n,
其中不正确的命题的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
已知两条相交直线a,b,a//平面a,则b与a的位置关系是( ).
A.b 平面a 平面a |
| B.b与平面a相交,或b∥平面a |
| C.b∥平面a |
| D.b⊥平面a |
已知直线l∥平面α,直线m Ìα,则直线l和m的位置关系是 .
(平行、相交、异面三种位置关系中选)
设 是空间三条直线,
是空间三条直线, 是空间两个平面,则下列命题中,逆命题不正确的是( )
是空间两个平面,则下列命题中,逆命题不正确的是( )
A.当 时,若 时,若 ,则 ,则 |
B.当 且 且 是 是 在 在 内的射影时,若 内的射影时,若 ,则 ,则 |
C.当 时,若 时,若 ,则 ,则 |
D.当 且 且 时,若 时,若 ,则 ,则 |
如图,三棱柱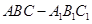 中,侧棱
中,侧棱 平面
平面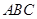 ,
,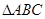 为等腰直角三角形,
为等腰直角三角形,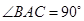 ,且
,且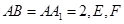 分别是
分别是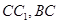 的中点.
的中点.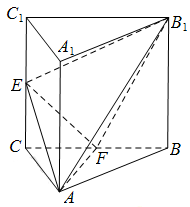
(1)求证: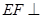 平面
平面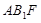 ;
;
(2)求锐二面角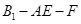 的余弦值;
的余弦值;
(3)若点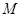 是
是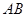 上一点,求
上一点,求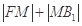 的最小值.
的最小值.
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点, D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF,正确的是( )

| A.(1)和(3) | B.(2)和(5) |
| C.(1)和(4) | D.(2)和(4) |
设 ,
, ,
, 是三个互不重合的平面,
是三个互不重合的平面, ,
, 是直线,给出下列命题:①
是直线,给出下列命题:① ,
, ,则
,则 ;②若
;②若 ,
, ,
, ,则
,则 ;③若
;③若 ,
, 在
在 内的射影互相垂直,则
内的射影互相垂直,则 ;④若
;④若 ,
, ,
, ,则
,则 ,其中正确命题的个数为( )
,其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
如图,三棱柱 中,侧棱
中,侧棱 底面
底面 ,底面三角形
,底面三角形 是正三角形,
是正三角形, 是
是 中点,则下列叙述正确的是
中点,则下列叙述正确的是
A. 与 与 是异面直线 是异面直线 |
B. 平面 平面 |
C. , , 为异面直线,且 为异面直线,且 |
D. 平面 平面 |
已知 为不同的直线,
为不同的直线, 为不同的平面,则下列说法正确的是
为不同的平面,则下列说法正确的是
A. |
B. |
C. |
D. |