 ,
, 为两个互相垂直的平面,a、b为一对异面直线,下列条件:
为两个互相垂直的平面,a、b为一对异面直线,下列条件:
①a// 、b
、b ;②a⊥
;②a⊥ 、b
、b ;③a⊥
;③a⊥ 、b
、b ;④a//
;④a// 、b
、b 且a与
且a与 的距离等于b与
的距离等于b与 的距离,其中是a⊥b的充分条件的有 ( )
的距离,其中是a⊥b的充分条件的有 ( ) 
| A.①④ | B.① | C.③ | D.②③ |
(本小题满分16分)如图,正四棱锥P-ABCD中,O是底面正方形的中心,E是PC的中点,求证
(1)PA∥平面BDE
(2)平面PAC  平面BDE
平面BDE
(设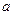 、
、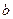 是两条不同的直线,α、β是两个不同的平面,则下列四个命题
是两条不同的直线,α、β是两个不同的平面,则下列四个命题
①若 ②若
②若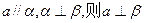
③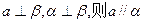 ④
④
其中正确的命题的个数是()
| A.0个 | B.1个 | C.2个 | D.3个 |
a、b是两条异面直线,则“a⊥b”是“存在经过a且与b垂直的平面”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件  既不充分也不必要条件
既不充分也不必要条件
如图甲,在△ABC中,AB⊥AC,AD⊥BC,
D是垂足,则AB2=BD·BC,该结论称为射
影定理。如图乙,在三棱锥A—BCD中,
AD⊥平面ABC,AO⊥平面BCD,O为垂
足,且O在△BCD内,类比射影定理,探
究S△BCO、S△BCD、S△ABC这三者之间满足的
关系式是 。
如图(1),△ 是等腰直角三角形,
是等腰直角三角形, E、F分别为AC、AB的中点,将△AEF沿EF折起,使
E、F分别为AC、AB的中点,将△AEF沿EF折起,使 在平面BCEF上的射影O恰好为EC的中点,得到图(2)。
在平面BCEF上的射影O恰好为EC的中点,得到图(2)。
(Ⅰ)求证: ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥 的体积。
的体积。

如图,直三棱柱ABC—A1B1C1中,AC=BC=1,∠ACB=90°,AA1= ,
,
D是A1B1中点.
(1)求证C1D⊥平面A1B;
(2)当点F在BB1上什么位置时,会使得AB1⊥平面C1DF?并证明你的结论.