如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n等于( ).
| A.8 | B.9 | C.10 | D.11 |
长方体的一 个顶点三条棱长分别为1,2,3,该长方体的顶点都在同一个球面上,则这个球的表面积为(s=4
个顶点三条棱长分别为1,2,3,该长方体的顶点都在同一个球面上,则这个球的表面积为(s=4 )()
)()
A. |
B.14 |
C.56 |
D.96 |
在三棱锥A—BCD中,侧棱AB、AC、AD两两垂直,△ABC、△ACD、△ADB的面积分别为 、
、 、
、 .则三棱锥A—BCD的外接球的体积为
.则三棱锥A—BCD的外接球的体积为
A. B.
B.

 D.
D.
如图所示,圆柱的高为2,底面半径为 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 ,四边形ABCD是正方形.
,四边形ABCD是正方形.
(Ⅰ)求证 ;
;
(Ⅱ)求四棱锥E-ABCD的体积.
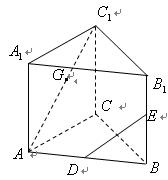
(本小题满分12分)如图,在正三棱柱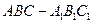 中,
中,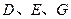 分别是
分别是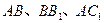 的中点,
的中点,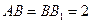 .
.
(Ⅰ)在棱 上是否存在点
上是否存在点 使
使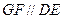 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;
(Ⅱ)求截面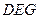 与底面
与底面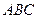 所成锐二面角的正切值;
所成锐二面角的正切值;
(Ⅲ)求点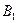 到截面
到截面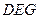 的距离.
的距离.
如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, .
.
(1)求证 ,并指出异面直线PA与CD所成角的大小;
,并指出异面直线PA与CD所成角的大小;
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 ?如果存在,求出此时三棱锥
?如果存在,求出此时三棱锥 与四棱锥
与四棱锥 的体积比;如果不存在,请说明理由.
的体积比;如果不存在,请说明理由.
若多面体的各个顶点都在同一球面上,则称这个多面体
内接于球.如图,设长方体 内接于球
内接于球
且
 则
则 两点之间的球面距离
两点之间的球面距离
为________.
已知梯形 中
中 ,
, ,
, ,
, 、
、 分别是
分别是 、
、 上的点,
上的点,
 ,
, .沿
.沿 将梯形
将梯形 翻折,使平面
翻折,使平面 ⊥平面
⊥平面 (如图).
(如图). 是
是 的中点.
的中点.
(1)当 时,求证:
时,求证: ⊥
⊥ ;
;
(2)当 变化时,求三棱锥
变化时,求三棱锥 体积的最大值.
体积的最大值.
如图,等边三角形 的中线
的中线 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 旋转过程中的一个图形,下列命题中,错误的是()
旋转过程中的一个图形,下列命题中,错误的是()
A.动点 在平面 在平面 上的射影在线段 上的射影在线段 上 上 |
B.恒有平面 ⊥平面 ⊥平面 |
C.三棱锥 的体积有最大值 的体积有最大值 |
D.异面直线 与 与 不可能垂直 不可能垂直 |
在三棱锥 中,
中, ,G为
,G为 的重心,过点G作三棱锥的一个截面,使截面平行于直线PB和AC,则截面的周长为.
的重心,过点G作三棱锥的一个截面,使截面平行于直线PB和AC,则截面的周长为.
如右图,在长方体 中, ,一质点从顶点 射向点 ,遇长方体的面反射(反射服从光的反射原理),将 次到第 次反射点之间的线段记为 , ,将线段 竖直放置在同一水平线上,则大致的图形是()





A B C D
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是________(写出所有正确命题的编号).
①当0<CQ<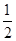 时,S为四边形;
时,S为四边形;
②当CQ=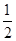 时,S为等腰梯形;
时,S为等腰梯形;
③当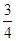 <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
④当CQ=1时,S的面积为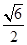 .
.