高中数学三角函数的恒等变换试题

已知函数 $f\left(x\right)={\sin }^{2}x+a\sin x\cos x-{\cos }^{2}x$，且 $f\left(\frac{\mathrm{\pi }}{4}\right)=1$.

（1）求常数a的值及 $f\left(x\right)$的最小值；
（2）当 $x\in \left[0,\frac{\mathrm{\pi }}{2}\right]$时，求 $f\left(x\right)$的单调增区间．

如图，半径为1的扇形中心角为 $\frac{\mathrm{\pi }}{3}$ ，一个矩形的一边在扇形的半径上，求此矩形的最大面积．

已知函数，其中，．若函数相邻两对称轴的距离等于．
（1）求的值；并求函数在区间的值域；
（2）在△中，、、分别是角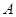、、的对边，若，求边、的长．

在△ABC中，内角A，B，C所对的边分别为a，b，c，已知△ABC的面积为3，b﹣c=2，cosA=﹣．
（Ⅰ）求a和sinC的值；
（Ⅱ）求cos（2A+）的值．

已知函数f（x）=2sinωxcosωx﹣2sin²ωx+（ω＞0），直线x=x₁，x=x₂是函数y=f（x）的图象的任意两条对称轴，且|x₁﹣x₂|的最小值为．
（Ⅰ）求ω的值；
（Ⅱ）求函数f（x）的单调增区间；
（Ⅲ）若f（α）=，求sin（π﹣4α）的值．

已知函数
（Ⅰ）求函数f（x）的定义域
（Ⅱ）若，求cosα的值
（Ⅲ）在（Ⅱ）条件下，若α是第四象限角，求的值．

已知，且，则 ．

设函数，其中，，若且图象的两条对称轴间的最近距离是．
（1）求函数的解析式；
（2）若是△的三个内角，且，求的取值范围．

（本小题满分14分）已知，
（Ⅰ）求的值 ，
（Ⅱ）求的值

已知，，则的值为（）

A．

B．

C．

D．

（本小题满分12分）在中，内角所对的边分别为，已知，.
（Ⅰ）求的值；
（Ⅱ）求的值.

已知函数
（1）求的值；
（2）求的递减区间.

已知函数，.
（1）求函数的最小正周期；
（2）求函数在区间上的值域.

如图在单位圆中，已知是坐标平面内的任意两个角，且，请写出两角差的余弦公式并加以证明.

如图所示，某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料，已知已有两面墙、的夹角为（即），现有可供建造第三面围墙的材料米（两面墙的长均大于米），为了使得仓库的面积尽可能大，记，问当为多少时，所建造的三角形露天仓库的面积最大，并求出最大值？