改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
| 支付金额 支付方式 |
不大于 元 |
大于 元 |
| 仅使用A |
27人 |
3人 |
| 仅使用B |
24人 |
1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于 元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于 元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于 元的人数有变化?说明理由.
从装有红球、黑球和白球的口袋中摸出一个球,若摸出的球是红球的概率是0.4,摸出的球是黑球的概率是0.25,那么摸出的球是白球或黑球的概率是( )
| A.0.35 | B.0.65 | C.0.1 | D.0.6 |
下列说法正确的是( )
A.某厂一批产品的次品率为 ,则任意抽取其中10件产品一定会发现一件次品 ,则任意抽取其中10件产品一定会发现一件次品 |
| B.气象部门预报明天下雨的概率是90%,说明明天该地区90%的地方要下雨,其余10%的地方不会下雨 |
| C.某医院治疗一种疾病的治愈率为10%,那么前9个病人都没有治愈,第10个人就一定能治愈 |
| D.掷一枚硬币,连续出现5次正面向上,第六次出现反面向上的概率与正面向上的概率仍然都为0.5 |
某人去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4.
(1)求他乘火车或乘飞机去的概率;
(2)求他不乘飞机去的概率;
(3)若他去的概率为0.5,请问他有可能是乘何种交通工具去的?
某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .
| |
第一批 |
第二批 |
第三批 |
| 女 |
196 |
x |
y |
| 男 |
204 |
156 |
z |
(1)求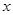 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
(3)已知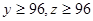 ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.
某食品企业一个月内被消费者投诉的次数用ξ表示,椐统计,随机变量ξ的概率分布如下: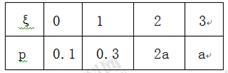
(Ⅰ)求a的值和ξ的数学期望;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
设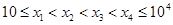 ,
,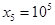 . 随机变量
. 随机变量 取值
取值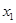 、
、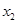 、
、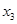 、
、 、
、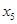 的概率均为0.2,随机变量
的概率均为0.2,随机变量 取值
取值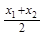 、
、 、
、 、
、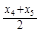 、
、 的概率也为0.2.若记
的概率也为0.2.若记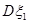 、
、 分别为
分别为 、
、 的方差,则 ( )
的方差,则 ( )
A.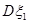 > > |
B.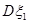 = = |
C.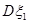 < < |
D.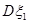 与 与 的大小关系与 的大小关系与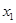 、 、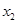 、 、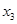 、 、 的取值有关 的取值有关 |
(本题14分)张老师居住在某城镇的A处,准备开车到学校B处上班。若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图。(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为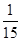 )。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量
)。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量 ,求
,求 的数学期望
的数学期望 。
。
下列说法:①随机事件 的概率是频率的稳定值,频率是概率的近似值;②一次试验中不同的基本事件不可能同时发生;③任意事件
的概率是频率的稳定值,频率是概率的近似值;②一次试验中不同的基本事件不可能同时发生;③任意事件 发生的概率
发生的概率 总满足
总满足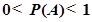 ;其中正确的是 ;(写出所有正确说法的序号)
;其中正确的是 ;(写出所有正确说法的序号)
某射手进行射击训练,假设每次射击击中目标的概率为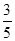 ,且每次射击的结果互不影响,已知射手射击了5
,且每次射击的结果互不影响,已知射手射击了5
次,求:
(1)其中只在第一、三、五次击中目标的概率;
(2)其中恰有3次击中目标的概率.
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?;
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3)根据数据推断A班全班40名学生中有几名学生的视力大于4.6?
小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只要答对其中两个问题,则闯关成功.每过一关可一次性获得价值分别为1000元,3000元,6000元的奖品(不重复得奖),小王对三关中每个问题回答正确的概率依次为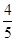 ,
,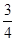 ,
,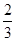 ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(1)求小王过第一关但未过第二关的概率;
(2)用X表示小王所获得奖品的价值,写出X的概率分布列,并求X的数学期望.
在高三的一个班中,有 的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,
的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5, ),则P(ξ=k)取最大值的k值为( )
),则P(ξ=k)取最大值的k值为( )
| A.0 | B.1 | C.2 | D.3 |
一个盒子里装有三张卡片,分别标记有数字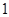 ,
,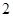 ,
,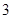 ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取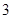 次,每次抽取
次,每次抽取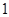 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为.
(Ⅰ)求"抽取的卡片上的数字满足"的概率;
(Ⅱ)求"抽取的卡片上的数字不完全相同"的概率.
[2013·课标全国卷Ⅱ]从1,2,3,4,5中任意取出两个不同的数,其和为5的概率是________.