已知一种材料的最佳加入量在100g到200g之间,若用0.618法安排试验,则第一次试点的加入量可以是 g.
为了比较注射
两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随即地分成两组。每组100只,其中一组注射药物
,另一组注射药物
.下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位:
)
表1:注射药物
后皮肤疱疹面积的频数分布表

表2:注射药物 后皮肤疱疹面积的频数分布表

(Ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
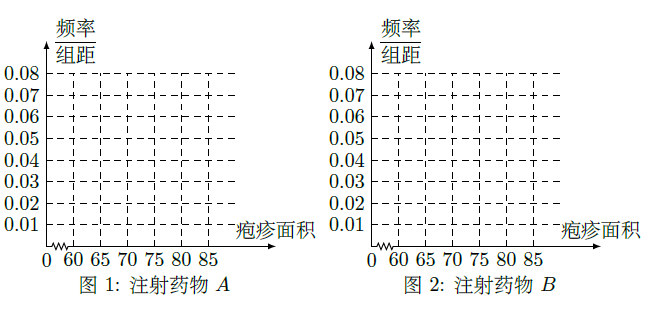
(Ⅱ)完成下面
列联表,并回答能否有99.9%的把握认为"注射药物
后的疱疹面积与注射药物
后的疱疹面积有差异".
表3:

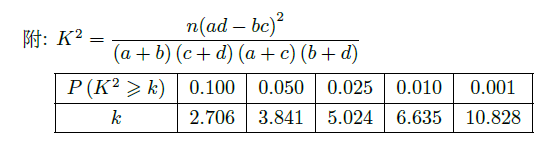
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:
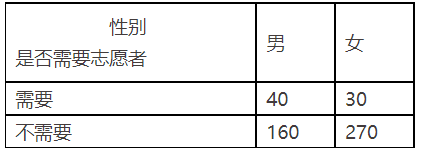
(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查办法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附:

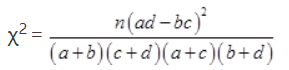
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则这10天甲、乙两人日加工零件的平均数分别为 和 .

为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
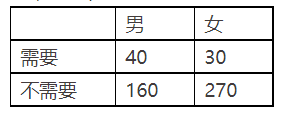
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有
的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由.
附:
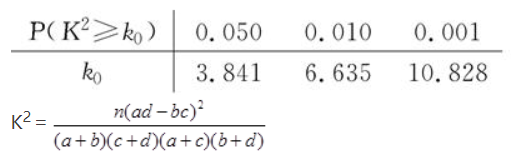
(本小题满分14分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
17.(本小题满分13分)
汽车是碳排放量比较大的行业之一.欧盟规定,从2012年开始,将对 排放量超过
排放量超过 的
的 型新车进行惩罚.某检测单位对甲、乙两类
型新车进行惩罚.某检测单位对甲、乙两类 型品牌车各抽取
型品牌车各抽取 辆进行
辆进行 排放量检测,记录如下(单位:
排放量检测,记录如下(单位: ).
).
| 甲 |
80 |
110 |
120 |
140 |
150 |
| 乙 |
100 |
120 |
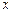 |
 |
160 |
经测算发现,乙品牌车 排放量的平均值为
排放量的平均值为
 .
.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆不符合 排放量的概率是多少?
排放量的概率是多少?
(Ⅱ)若 ,试比较甲、乙两类品牌车
,试比较甲、乙两类品牌车 排放量的稳定性.
排放量的稳定性.
对于两个变量之间的相关系数,下列说法中正确的是( )
A. , ,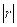 越大,相关程度越大, 越大,相关程度越大, 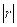 越小,相关程度越小 越小,相关程度越小 |
B. , ,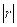 越大,相关程度越小, 越大,相关程度越小,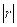 越小,相关程度越大 越小,相关程度越大 |
C.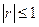 且 且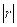 越接近于 越接近于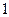 ,相关程度越大; ,相关程度越大;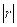 越接近于 越接近于 ,相关程度越小 ,相关程度越小 |
D.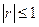 且 且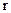 >0比 >0比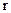 <0相关程度大; <0相关程度大; |
测得某国家10对父子身高(单位:英寸)如下:
| 父亲身高(x) |
60 |
62 |
64 |
65 |
66 |
67 |
68 |
70 |
72 |
74 |
| 儿子身高(y) |
63.6 |
65.2 |
66 |
65.5 |
66.9 |
67.1 |
67.4 |
68.3 |
70.1 |
70 |
(1)对变量y与x进行相关性检验;
(2)如果y与x之间具有线性相关关系,求回归直线方程;
(3)如果父亲的身高为73英寸,估计儿子的身高.
某地10户家庭的年收入和年饮食支出的统计资料如下表:
| 年收入 x(万元) |
2 |
4 |
4 |
6 |
6 |
6 |
7 |
7 |
8 |
10 |
| 年饮食支出 y(万元) |
0.9 |
1.4 |
1.6 |
2.0 |
2.1 |
1.9 |
1.8 |
2.1 |
2.2 |
2.3 |
(1)根据表中数据,确定家庭的年收入和年饮食支出之间是否具有相关关系;若具有相关关系求出y与x的回归直线方程;
(2)如果某家庭年收入为9万元,预测其年饮食支出.
某公司利润y与销售总额x(单位:千万元)之间有如下对应数据:
| x |
10 |
15 |
17 |
20 |
25 |
28 |
32 |
| y |
1 |
1.3 |
1.8 |
2 |
2.6 |
2.7 |
3.3 |
(1)画出散点图;
(2)求回归直线方程;
(3)估计销售总额为24千万元时的利润.
某企业上半年产品产量与单位成本资料如下:
| 月份 |
产量(千件) |
单位成本(元) |
| 1 |
2 |
73 |
| 2 |
3 |
72 |
| 3 |
4 |
71 |
| 4 |
3 |
73 |
| 5 |
4 |
69 |
| 6 |
5 |
68 |
(1)求出线性回归方程;
(2)指出产量每增加1 000件时,单位成本平均变动多少?
(3)假定产量为6 000件时,单位成本为多少元?