下表为某班5位同学身高x(单位:cm)与体重y(单位kg)的数据,
| 身高 |
170 |
171 |
166 |
178 |
160 |
| 体重 |
75 |
80 |
70 |
85 |
65 |
若两个量间的回归直线方程为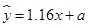 ,则身高为185cm的学生的体重约为( )
,则身高为185cm的学生的体重约为( )
A.87.6kg B.89.5kg C.91.4kg D.92.3kg
某咖啡厂为了了解热饮的销售量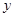 (个)与气温
(个)与气温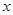 (℃)之间的关系,随机统计了某4天的销售量与气温,并制作了对照表:
(℃)之间的关系,随机统计了某4天的销售量与气温,并制作了对照表:
| 气温(℃) |
18 |
13 |
10 |
-1 |
| 销售量个) |
24 |
34 |
38 |
64 |
由表中数据,得线性回归方程为y= x
x ,,当气温为-4℃时,预测销售量约为
,,当气温为-4℃时,预测销售量约为
A.68 B.66 C.72 D.70
四名同学根据各自的样本数据研究变量 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且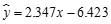 ;
;
②y与x负相关且 ;
;
③y与x正相关且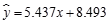 ;
;
④y与x正相关且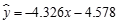 .
.
其中一定不正确的结论的序号是 ( )
| A.①② | B.②③ | C.③④ | D.①④ |
【改编题】已知x,y的值如下表所示:
| x |
2 |
3 |
4 |
| y |
5 |
4 |
6 |
如果y与x呈线性相关,则回归方程为 所表示的直线经过的定点为_______.
所表示的直线经过的定点为_______.
已知某企业上半年前5个月产品广告投入与利润额统计如下:
| 月份 |
1 |
2 |
3 |
4 |
5 |
| 广告投入(x万元) |
9.5 |
9.3 |
9.1 |
8.9 |
9.7 |
| 利润(y万元) |
92 |
89 |
89 |
87 |
93 |
由此所得回归方程为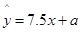 ,若6月份广告投入10万元,估计所获得利润为( )
,若6月份广告投入10万元,估计所获得利润为( )
A.95.25万元 B.96.5万元 C.97万元 D.97.25万元
一个车间为了规定工作定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
由表中数据,求得线性回归方程 ,根据回归方程,
,根据回归方程,
预测加工70个零件所花费的时间为 分钟.
某单位为了了解用电量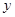 (度)与当天平均气温
(度)与当天平均气温 (°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程
(°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程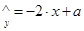 ,则
,则 __________.
__________.
平均气温 (°C) (°C) |
18 |
13 |
10 |
-1 |
用电量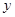 (度) (度) |
25 |
35 |
37 |
63 |
若两个分类变量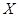 和
和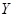 的
的 列联表为:
列联表为:
| |
 |
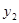 |
合计 |
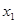 [ [ |
10 |
40 |
50 |
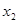 |
20 |
30 |
50 |
| 合计 |
30 |
70 |
100 |
参考公式:独立性检测中,随机变量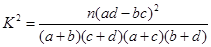
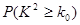 |
… |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
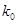 |
… |
2.706 |
3.841 |
5.0240 |
6.635 |
7.879 |
10.828 |
则认为“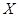 与
与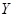 之间有关系”的把握可以达到 ( )
之间有关系”的把握可以达到 ( )
A. B.
B. C.
C.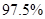 D.
D.
下列关于回归分析的说法正确的是 (填上所有正确说法的序号)
①相关系数 越小,两个变量的相关程度越弱;②残差平方和越大的模型,拟合效果越好;③用相关指数
越小,两个变量的相关程度越弱;②残差平方和越大的模型,拟合效果越好;③用相关指数 来刻画回归效果时,
来刻画回归效果时, 越小,说明模型的拟合效果越好;④用最小二乘法求回归直线方程,是寻求使
越小,说明模型的拟合效果越好;④用最小二乘法求回归直线方程,是寻求使 取最小值时的
取最小值时的 的值;⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
的值;⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:由上表可得回归直线方程 中的
中的 ,据此模型预测零售价为15元时,每天的销售量为 .
,据此模型预测零售价为15元时,每天的销售量为 .

人们在生活和消费过程中的过量碳排放,是造成全球气候变暖的重要因素之一,所谓“低碳生活”就是指生活作息时所耗用的能量要尽力减少,从而减低二氧化碳的排放量.某单位为了制定节能减排的目标,先调查了用电量 (度)与气温
(度)与气温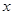 (
(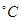 )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温(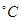 ) ) |
18 |
13 |
10 |
 |
| 用电量(度) |
24 |
34 |
38 |
64 |
由表中数据,得线性回归方程 ,当气温为
,当气温为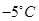 时,预测用电量的度数约为 .
时,预测用电量的度数约为 .
某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
| |
认为作业多 |
认为作业不多 |
总数 |
| 喜欢玩电脑游戏 |
18 |
9 |
27 |
| 不喜欢玩电脑游戏 |
8 |
15 |
23 |
| 总数 |
26 |
24 |
50 |
根据表中数据得到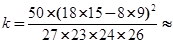 5.059,因为p(K
5.059,因为p(K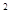 ≥5.024)=0.025,
≥5.024)=0.025,
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )
(A)97.5% (B) 95% (C)90% (D)无充分根据
(本小题满分10分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出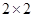 列联表,并判断是否有
列联表,并判断是否有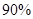 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
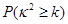 |
0.100 |
0.050 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
6.635 |
10.828 |
 .
.
已知变量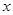 与
与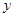 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
,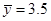 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.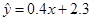 |
B.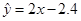 |
C.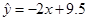 |
D.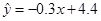 |