高中数学函数的基本性质试题

已知函数，.
(1)a≥－2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为,其中,求的最小值.

定义在上的函数，如果满足：对任意，存在常数，都有成立，则称是上的有界函数，其中称为函数的一个上界．已知函数，．
（1）若函数为奇函数，求实数的值；
（2）在（1）的条件下，求函数在区间上的所有上界构成的集合；
（3）若函数在上是以3为上界的有界函数，求实数的取值范围．

设函数f(x)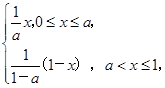＝a为常数且a∈(0，1)．
(1)当a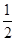＝时，求f；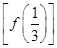
(2)若x₀满足f[f(x₀)]＝x₀，但f(x₀)≠x₀，则称x₀为f(x)的二阶周期点．证明函数f(x)有且仅有两个二阶周期点，并求二阶周期点x₁，x₂；
(3)对于(2)中的x₁，x₂，设A(x₁，f[f(x₁)])，B(x₂，f[f(x₂)])，C(a²，0)，记△ABC的面积为S(a)，求S(a)在区间[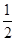，]上的最大值和最小值．

已知函数，．
（1）若，判断函数的奇偶性，并加以证明；
（2）若函数在上是增函数，求实数的取值范围；
（3）若存在实数使得关于的方程有三个不相等的实数根，求实数的取值范围．

定义在上的函数同时满足以下条件：
①在(0,1)上是减函数，在(1，＋∞)上是增函数；
②是偶函数；
③在x＝0处的切线与直线y＝x＋2垂直．
(1)求函数＝的解析式；
(2)设g(x)＝，若存在实数x∈[1，e]，使<，求实数m的取值范围．.

已知函数.
（Ⅰ）当，函数有且仅有一个零点，且时，求的值；
（Ⅱ）若函数在区间上为单调函数，求的取值范围.

已知实数，函数.
（1）当时，求的最小值;
（2）当时,判断的单调性,并说明理由；
（3）求实数的范围，使得对于区间上的任意三个实数，都存在以为边长的三角形.

已知函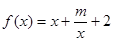数（为实常数）．
（1）若函数图像上动点到定点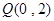的距离的最小值为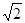，求实数的值；
（2）若函数在区间上是增函数，试用函数单调性的定义求实数的取值范围；
（3）设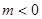，若不等式在有解，求的取值范围．

已知函数且，其中为奇函数, 为偶函数，若不等式对任意恒成立,则实数的取值范围是.

现有两个命题：
（1）若，且不等式恒成立，则的取值范围是集合；
（2）若函数，的图像与函数的图像没有交点，则的取值范围是集合；
则以下集合关系正确的是（）

A．

B．

C．

D．