下列函数中,在区间(0,+∞)上为增函数的是()
A. |
B. |
C. |
D. |
设函数 ,则 是()
| A. | 奇函数,且在(0,1)上是增函数 |
| B. | 奇函数,且在(0,1)上是减函数 |
| C. | 偶函数,且在(0,1)上是增函数 |
| D. | 偶函数,且在(0,1)上是减函数 |
若函数 是定义在
是定义在 上的偶函数,则该函数的最大值为
上的偶函数,则该函数的最大值为
| A.5 | B.4 | C.3 | D.2 |
(本小题满分12分)
已知函数 .
.
(1)求函数 的定义域及
的定义域及 的值;
的值;
(2)判断函数 的奇偶性;
的奇偶性;
(3)判断 在(0,+∞)上的单调性,并给予证明.
在(0,+∞)上的单调性,并给予证明.
函数 的定义域为A,若
的定义域为A,若 且
且 时总有
时总有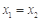 ,则称
,则称 为单函数.例如,函数
为单函数.例如,函数 =2x+1(
=2x+1( )是单函数.下列命题:
)是单函数.下列命题:
①函数 (x
(x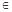 R)是单函数;
R)是单函数;
②指数函数 (x
(x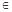 R)是单函数;
R)是单函数;
③若 为单函数,
为单函数, 且
且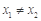 ,则
,则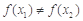 ;
;
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是_________.(写出所有真命题的编号)
函数 在[0,2]上单调递增,且函数
在[0,2]上单调递增,且函数 是偶函数,则下列结论成立的是()
是偶函数,则下列结论成立的是()
A.f(1)<f( )<f( )<f( ) ) |
B.f( )<f(1)<f( )<f(1)<f( ) ) |
C.f( )<f( )<f( )<f(1) )<f(1) |
D.f( )<f(1)<f( )<f(1)<f( ) ) |
 为实数,
为实数, 表示不超过
表示不超过 的最大整数,则函数
的最大整数,则函数 在
在 上为
上为
| A.增函数 | B.周期函数 | C.奇函数 | D.偶函数 |
函数 ,给出以下命题:
,给出以下命题:
①函数 有
有 个零点;
个零点;
②若 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 ;
;
③函数 的极大值中一定存在最小值;
的极大值中一定存在最小值;
④
 ,对一切
,对一切 恒成立;
恒成立;
⑤任取 ,
, ,都有
,都有 恒成立.
恒成立.
其中真命题的有
【改编题】已知 在
在 上单调递增,那么实数
上单调递增,那么实数 的取值范围是()
的取值范围是()
A. |
B. |
C. |
D. |
若 是奇函数,且在
是奇函数,且在 上是减函数,又有
上是减函数,又有 ,则不等式
,则不等式 的解集为()
的解集为()
A. |
B. |
C. |
D. |