给出下列四个命题:
①命题“ ”的否定是“
”的否定是“ ”;
”;
②“ ”是“直线
”是“直线 与直线
与直线 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
③设圆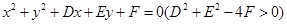 与坐标轴有4个交点,分别为
与坐标轴有4个交点,分别为 ,则
,则 ;
;
④关于 的不等式
的不等式 的解集为
的解集为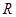 ,则
,则 .
.
其中所有真命题的序号是 .
下列结论:
①已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是 =-3;
=-3;
②命题“设a,b∈R,若a+b≠6,则a≠3或b≠3”是一个假命题;
③函数 是奇函数;
是奇函数;
④在△ABC中,若sinAcosB=sinC,则△ABC是直角三角形;
⑤“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的充要条件;
⑥已知a、b为平面上两个不共线的向量,p:|a+2b|=|a-2b|;q:a⊥b,则p是q的必要不充分条件.其中正确结论的序号为________.
已知集合A={x|x>5},集合B={x|x>a},若命题“x∈A”是命题“x∈B”的充分不必要条件,则实数a的取值范围是________.
某健康中心研究认为:身高为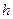 (cm)的人的其理想体重
(cm)的人的其理想体重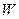 (kg),应符合公式
(kg),应符合公式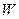 =22
=22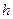 2 (kg),且定义体重在理想体重±10%的范围内,称为标准体重;超过10%但不超过20%者,称为微胖;超过20%者,称为肥胖, 微胖及肥胖都是过重的现象. 对身高
2 (kg),且定义体重在理想体重±10%的范围内,称为标准体重;超过10%但不超过20%者,称为微胖;超过20%者,称为肥胖, 微胖及肥胖都是过重的现象. 对身高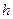 ,体重
,体重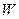 的人,体重过重的充要条件为
的人,体重过重的充要条件为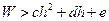 ,则
,则 __________
__________
平面内两直线有三种位置关系:相交,平行与重合.已知两个相交平面 与两直线 ,又知 在 内的射影为 ,在 内的射影为 .试写出 与 满足的条件,使之一定能成为 是异面直线的充分条件.