已知椭圆C: +
+ =1
=1 的离心率为
的离心率为 ,左焦点为F(-1,0),
,左焦点为F(-1,0),
(1)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线L与椭圆C交于M,N两点,若 ,求直线L的方程;
,求直线L的方程;
(2)椭圆C上是否存在三点P,E,G,使得S△OPE=S△OPG=S△OEG= ?
?
已知椭圆C: (a>b>0),过点(0,1),且离心率为
(a>b>0),过点(0,1),且离心率为 .
.
(1)求椭圆C的方程;
(2)A,B为椭圆C的左右顶点,直线l:x=2 与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,
与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时, 恒为定值.
恒为定值.
己知a∈R,函数
(1)若a=1,求曲线 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;
(2)若|a|>1,求 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值.
设函数 ,其中b≠0.
,其中b≠0.
(1)当b> 时,判断函数
时,判断函数 在定义域上的单调性:
在定义域上的单调性:
(2)求函数 的极值点.
的极值点.
设各项都是正整数的无穷数列 满足:对任意
满足:对任意 ,有
,有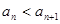 .记
.记 .
.
(1)若数列 是首项
是首项 ,公比
,公比 的等比数列,求数列
的等比数列,求数列 的通项公式;
的通项公式;
(2)若 ,证明:
,证明: ;
;
(3)若数列 的首项
的首项 ,
, ,
, 是公差为1的等差数列.记
是公差为1的等差数列.记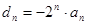 ,
, ,问:使
,问:使 成立的最小正整数
成立的最小正整数 是否存在?并说明理由.
是否存在?并说明理由.
已知椭圆
 的右焦点为
的右焦点为
 ,短轴的端点分别为
,短轴的端点分别为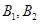 ,且
,且 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 且斜率为
且斜率为
 的直线
的直线 交椭圆于
交椭圆于 两点,弦
两点,弦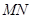 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点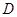 .设弦
.设弦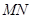 的中点为
的中点为 ,试求
,试求 的取值范围.
的取值范围.
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧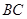 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧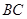 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.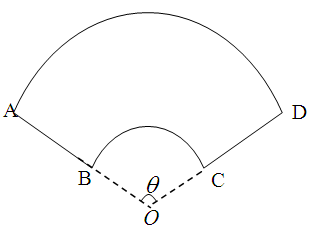
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?
如图,四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, ,
, 平面
平面 ,
, ,
, ,
, 是
是 的中点.
的中点.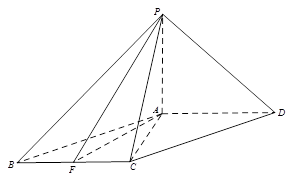
(1)求证: 平面
平面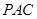 ;
;
(2)若以 为坐标原点,射线
为坐标原点,射线 、
、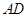 、
、 分别是
分别是 轴、
轴、 轴、
轴、 轴的正半轴,建立空间直角坐标系,已经计算得
轴的正半轴,建立空间直角坐标系,已经计算得 是平面
是平面 的法向量,求平面
的法向量,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
已知椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,且椭圆C上一点与两个焦点F1,F2构成的三角形的周长为2
,且椭圆C上一点与两个焦点F1,F2构成的三角形的周长为2 +2.
+2.
(1)求椭圆C的方程;
(2)过右焦点F2作直线l 与椭圆C交于A,B两点,设 ,若
,若 ,求
,求 的取值范围.
的取值范围.
已知函数 在(0,1)上单调递减.
在(0,1)上单调递减.
(1)求a的取值范围;
(2)令 ,求
,求 在[1,2]上的最小值.
在[1,2]上的最小值.
已知等差数列{an}的前n项和为Sn,S7=49,a4和a8的等差中项为2.
(1)求an及Sn;
(2)证明:当n≥2时,有 .
.
已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点,设左右焦点分别为F1,F2,P是C1与C2在第一象限的交点,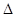 PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
A.(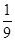 ,+ ,+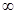 ) ) |
B.(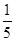 ,+ ,+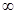 ) ) |
C.(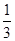 ,+ ,+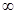 ) ) |
D.(0,+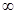 ) ) |
设函数 的定义域是
的定义域是 ,其中常数
,其中常数 .(注:
.(注: 
(1)若 ,求
,求 的过原点的切线方程.
的过原点的切线方程.
(2)证明当 时,对
时,对 ,恒有
,恒有 .
.
(3)当 时,求最大实数
时,求最大实数 ,使不等式
,使不等式 对
对 恒成立.
恒成立.