高中数学试题

已知α∈（0， $\frac{\pi }{2}$ ），tanα＝2，则cos（α $-\frac{\pi }{4}$ ）＝      ．

曲线 y＝ x ² $+\frac{1}{x}$ 在点（1，2）处的切线方程为 　 　．

已知向量 $\stackrel{\to }{a}=$ （﹣1，2）， $\stackrel{\to }{b}=$ （ m，1），若向量 $\stackrel{\to }{a}+\stackrel{\to }{b}$ 与 $\stackrel{\to }{a}$ 垂直，则 m＝ 　　．

设 A， B是椭圆 C： $\frac{x^2}{3}+\frac{y^2}{m}=$ 1长轴的两个端点，若 C上存在点 M满足∠ AMB＝120°，则 m的取值范围是（　　）

A．	（0，1]∪[9，+∞）	B．	（0， $\sqrt{3}$ ]∪[9，+∞）
C．	（0，1]∪[4，+∞）	D．	（0， $\sqrt{3}$ ]∪[4，+∞）

△ ABC的内角 A， B， C的对边分别为 a， b， c，已知sin B+sin A（sin C﹣cos C）＝0， a＝2， c $=\sqrt{2}$ ，则 C＝（　　）

A．

$\frac{\pi }{12}$

B．

$\frac{\pi }{6}$

C．

$\frac{\pi }{4}$

D．

$\frac{\pi }{3}$

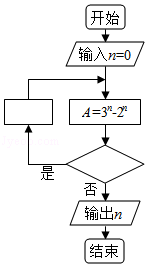
如图程序框图是为了求出满足3 ⁿ﹣2 ⁿ＞1000的最小偶数 n，那么在 和 两个空白框中，可以分别填入（　　）

A．	A＞1000和n＝n+1	B．	A＞1000和n＝n+2
C．	A≤1000和n＝n+1	D．	A≤1000和n＝n+2

已知函数 f（ x）＝ lnx+ ln（2﹣ x），则（　　）

A．	f（x）在（0，2）单调递增
B．	f（x）在（0，2）单调递减
C．	y＝f（x）的图象关于直线x＝1对称
D．	y＝f（x）的图象关于点（1，0）对称

函数 y $=\frac{\mathit{sin}2x}{1-\mathit{cosx}}$ 的部分图象大致为（　　）

A．
B．
C．
D．

设 x， y满足约束条件 $\left\{\begin{array}{c}x+3y\le 3\\ x-y\ge 1\\ y\ge 0\end{array}\right.$ ，则 z＝ x+ y的最大值为（　　）

A．

0

B．

1

C．

2

D．

3

如图，在下列四个正方体中， A， B为正方体的两个顶点， M， N， Q为所在棱的中点，则在这四个正方体中，直线 AB与平面 MNQ不平行的是（　　）

A．		B．
C．		D．

已知 F是双曲线 C： x ² $-\frac{y^2}{3}=$ 1的右焦点， P是 C上一点，且 PF与 x轴垂直，点 A的坐标是（1，3），则△ APF的面积为（　　）

A．

$\frac{1}{3}$

B．

$\frac{1}{2}$

C．

$\frac{2}{3}$

D．

$\frac{3}{2}$

如图，正方形 ABCD内的图形来自中国古代的太极图．正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（　　）

A．

$\frac{1}{4}$

B．

$\frac{\pi }{8}$

C．

$\frac{1}{2}$

D．

$\frac{\pi }{4}$

下列各式的运算结果为纯虚数的是（　　）

A．

i（1+i） ^2

B．

i ^2（1﹣i）

C．

（1+i） ^2

D．

i（1+i）

为评估一种农作物的种植效果，选了 n块地作试验田．这 n块地的亩产量（单位： kg）分别是 x ₁， x ₂，…， x _n，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是（　　）

A．	x 1，x 2，…，x n的平均数	B．	x 1，x 2，…，x n的标准差
C．	x 1，x 2，…，x n的最大值	D．	x 1，x 2，…，x n的中位数

已知集合 A＝{ x| x＜2}， B＝{ x|3﹣2 x＞0}，则（　　）

A．

A∩B＝{x|x $＜\frac{3}{2}$ }

B．

A∩B＝∅

C．

A∪B＝{x|x $＜\frac{3}{2}$ }

D．

A∪B＝R