设全集为R, ,
, ,
, .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)若 ,求实数a的取值范围.
,求实数a的取值范围.
如果对定义在R上的函数 ,对任意两个不相等的实数
,对任意两个不相等的实数 ,都有
,都有 ,则称函数
,则称函数 为“H函数”.给出下列函数①
为“H函数”.给出下列函数① ;②
;② ;③
;③ ;④
;④ .以上函数是“H函数”的所有序号为 .
.以上函数是“H函数”的所有序号为 .
观察分析下表中的数据:

猜想一般凸多面体中F,V,E所满足的等式是 .
有6个大小相同的黑球,编号为1,2,3,4,5,6,还有4个同样大小的白球,编号为7,8,9,10,现从中任取4个球,有如下集中变量:①X表示取出的最大号码;②Y表示取出的最小号码;③取出一个黑球记2分,取出一个白球记1分,ξ表示取出的4个球的总得分;④η表示取出的黑球个数,这四种变量中服从超几何分布的是( )
| A.①② | B.③④ | C.①②④ | D.①②③④ |
已知随机变量ξ服从正态分布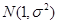 .若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为( )
.若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为( )
| A.0.8 | B.0.6 | C.0.5 | D.0.4 |
下面给出了关于复数的三种类比推理:其中类比错误的是( )
①复数的乘法运算法则可以类比多项式的乘法运算法则;
②由向量 的性质
的性质 可以类比复数的性质
可以类比复数的性质 ;
;
③由向量加法的几何意义可以类比得到复数加法的几何意义.
| A.② | B.①② | C.①③ | D.③ |
把正奇数数列 中的数按上小下大、左小右大的原则排成如图的三角形数表:
中的数按上小下大、左小右大的原则排成如图的三角形数表:
设
 是位于这个三角形数表中从上往下数第m行、从左往右数第n个数.
是位于这个三角形数表中从上往下数第m行、从左往右数第n个数.
(1)求 ;
;
(2)若 ,求m,n的值;
,求m,n的值;
(3)已知函数 ,若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和
,若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和 .
.
已知二次函数 :
:
(1)若函数在区间 上存在零点,求实数q的取值范围;
上存在零点,求实数q的取值范围;
(2)问:是否存在常数t( ),当
),当 时,
时, 的值域为区间D,且D的长度为
的值域为区间D,且D的长度为 .
.