把正奇数数列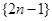 中的数按上小下大、左小右大的原则排成如图的三角形数表:
中的数按上小下大、左小右大的原则排成如图的三角形数表:
设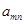
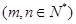 是位于这个三角形数表中从上往下数第m行、从左往右数第n个数.
是位于这个三角形数表中从上往下数第m行、从左往右数第n个数.
(1)求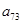 ;
;
(2)若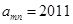 ,求m,n的值;
,求m,n的值;
(3)已知函数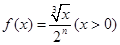 ,若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和
,若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和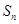 .
.
推荐套卷
把正奇数数列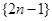 中的数按上小下大、左小右大的原则排成如图的三角形数表:
中的数按上小下大、左小右大的原则排成如图的三角形数表:
设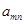
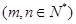 是位于这个三角形数表中从上往下数第m行、从左往右数第n个数.
是位于这个三角形数表中从上往下数第m行、从左往右数第n个数.
(1)求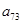 ;
;
(2)若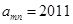 ,求m,n的值;
,求m,n的值;
(3)已知函数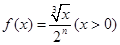 ,若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和
,若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和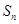 .
.