若z=1+ i,则|z 2-2 z|=( )
| A. |
0 |
B. |
1 |
C. |
|
D. |
2 |
将数列{2n–1}与{3n–2}的公共项从小到大排列得到数列{an},则{an}的前n项和为________.
斜率为 的直线过抛物线C:y2=4x的焦点,且与C交于A,B两点,则 =________.
已知 P是边长为2的正六边形 ABCDEF内的一点,则 的取值范围是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
基本再生数 R 0与世代间隔 T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型: 描述累计感染病例数 I( t)随时间 t(单位:天)的变化规律,指数增长率 r与 R 0, T近似满足 R 0=1+ rT.有学者基于已有数据估计出 R 0=3.28, T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )
| A. |
1.2天 |
B. |
1.8天 |
| C. |
2.5天 |
D. |
3.5天 |
某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
| A. |
62% |
B. |
56% |
| C. |
46% |
D. |
42% |
6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
| A. |
120种 |
B. |
90种 |
| C. |
60种 |
D. |
30种 |
设集合 A={ x|1≤ x≤3}, B={ x|2< x<4},则 A∪ B=( )
| A. |
{x|2<x≤3} |
B. |
{x|2≤x≤3} |
| C. |
{x|1≤x<4} |
D. |
{x|1<x<4} |
在极坐标系中,已知点 在直线 上,点 在圆 上(其中 , ).
(1)求 , 的值
(2)求出直线 与圆 的公共点的极坐标.
平面上点 在矩阵 对应的变换作用下得到点 .
(1)求实数 , 的值;
(2)求矩阵 的逆矩阵 .
将函数y= 的图象向右平移 个单位长度,则平移后的图象中与y轴最近的对称轴的方程是____.
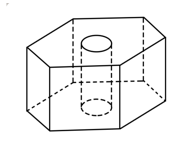
如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半轻为0.5 cm,则此六角螺帽毛坯的体积是____cm.