利用计算机产生0~1之间的均匀随机数a,则事件“3a-1>0”发生的概率为 .
给定两个命题p,q.若﹁p是q的必要而不充分条件,则p是﹁q的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知集合M={x|(x-1)2<4,x∈R},N={-1,0,1,2,3},则M∩N=( )
| A.{0,1,2} | B.{-1,0,1,2} | C.{-1,0,2,3} | D.{0,1,2,3} |
口袋中有n(n∈N*)个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X,若P(X=2)=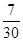 求:
求:
(1)n的值;
(2)X的概率分布与数学期望.
定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(-1,4]时,f(x)=x2-2x,则函数f(x)在[0,2013]上的零点个数是_____ .