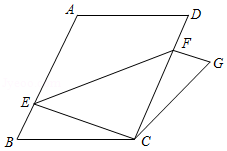
如右图,在 中, 、 分别是 、 延长线上的点,且 ,连接 交 、 于点 、 .求证: .

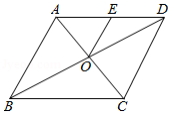
如图,四边形 为平行四边形, 、 为 边的两个三等分点,连接 、 交于点 ,则

A. B. C. D.
如图,在 中,分别以边 , 作等腰 , ,使 , , ,连接 , .
(1)求证 ;
(2)延长 与 相交于 .若 ,求证 .

如图,在平行四边形 中, , , 是锐角, 于点 , 是 的中点,连结 、 .若 ,则 长为

A.2B. C. D.
如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形, 经过点 ,连接 交 于点 ,观察发现:点 是 的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接 交 于点 .
请参考上面的思路,证明点 是 的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当 时,延长 、 交于点 ,求 的值;
(3)在(2)的条件下,若 为大于 的常数),直接用含 的代数式表示 的值.

如图,在平行四边形 中, 的平分线交 于点 ,交 于点 ,交 的延长线于点 ,若 ,则 的值为

A. B. C. D.
如图, 的对角线 、 相交于点 , 交 于点 ,若 , 的周长等于5,则 的周长等于 .
点 是平行四边形 的对角线 所在直线上的一个动点(点 不与点 、 重合),分别过点 、 向直线 作垂线,垂足分别为点 、 .点 为 的中点.
(1)如图1,当点 与点 重合时,线段 和 的关系是 ;
(2)当点 运动到如图2所示的位置时,请在图中补全图形并通过证明判断(1)中的结论是否仍然成立?
(3)如图3,点 在线段 的延长线上运动,当 时,试探究线段 、 、 之间的关系.

如图,将平行四边形纸片 沿一条直线折叠,使点 与点 重合,点 落在点 处,折痕为 .求证:
(1) ;
(2) .