高中物理探究单摆的周期与摆长的关系试题

下面是用单摆测定重力加速度实验中获得的有关数据：

摆长l/m	0.5	0.6	0.8	1.1
周期T^2/s^2	2.2	2.5	3.2	4.5

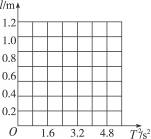
图11-4
（1）利用上述数据在坐标图中描出l-T²图象.
（2）利用图象，取T²=0.1×4π²s²=3.95s²，求重力加速度.

一个秒摆摆球的质量为0.2 kg，它振动到最大位移时距最低点的高度为0.4 cm，它完成10次全振动回到最大位移时，距最低点的高度变为0.3 cm，如果每完成10次全振动给它补充一次能量，使摆球回到原来的高度，在60 s内总共补充的能量是____________________.

利用高楼楼顶下垂的单摆、实验室用的刻度尺和秒表，如何测定当地的重力加速度？请你设计一种行之有效的方法，写出简要的实验原理及计算g值的公式.（注意：单摆摆长无法直接测出）

为了使单摆做简谐运动的周期变长，可以使（    )

A．单摆的振幅适当加大	B．单摆的摆长适当加长
C．单摆从山下移到山上	D．单摆从北京移到南极

如图1-1所示，A、B分别为单摆做简谐运动时摆球的不同位置.其中，位置A为摆球摆动的最高位置，虚线为过悬点的竖直线.以摆球最低位置为重力势能零点，则摆球在摆动过程中

图1-1
A.位于B处时动能最大
B.位于A处时势能最大
C.在位置A的势能大于在位置B的动能
D.在位置B的机械能大于在位置A的机械能

在“用单摆测定重力加速度”的实验中，用刻度尺测量悬点到小球的距离为96.60 cm，用卡尺量得小球直径是5.260 cm，测量周期有3次，每次是在摆球通过最低点时，按下秒表开始计时，同时将此次通过最低点作为第一次，接着一直数到计时终止，结果如下表.

	1	2	3
数的次数	61	81	71
时间（s）	60.40	79.80	70.60

这个单摆振动周期的测定值是_______________s，当地重力加速度的值是__________m/s².（取三位有效数字）

某同学在“利用单摆测重力加速度”的实验中，先测得摆线长为97.50 cm，摆球直径为2.00 cm，然后用秒表记录了单摆振动50次所用的时间，如图11-4所示，则

图11-4
（1）该摆摆长为 ____________cm，秒表所示读数为____________s.
（2）如果他测得的g值偏小，可能的原因是____________.

A．测摆线长时测了悬线的总长度

B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了，使周期变大了

C．开始计时时，秒表过迟按下

D．实验中误将49次全振动数次数记为50次

（3）为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l与T的数据如图11-5，再以l为横坐标，T²为纵坐标将所得数据连成直线，并求得该直线的斜率为k，则重力加速度g=________________.（用k表示）

图11-5

如图1-8所示，密度为0.8×10³ kg/m³的木球由长l="100" cm的细绳固定在水中，将木球拉离平衡位置一很小角度后释放，水的粘滞阻力不计，木球摆动的周期多大？

图1-8

如图1-5所示，两根长度均为L的细线下端拴一质量为m的小球，两线间夹角为α,今使摆球在垂直纸面的平面内做小幅度振动，求其振动频率.

图1-5

在青岛调准的摆钟,随南极考察船到达南极,这个摆钟

A．变慢了	B．变快了,应减小摆长
C．不变	D．变快了,应加大摆长

如图1-1所示，是一个单摆的共振曲线(取g="10" m/s²)

A．此单摆的摆长约为2.8 m	B．此单摆的周期约为0.3 s
C．若摆长增大，共振曲线的峰将向上移动	D．若摆长增大，共振曲线的峰将向左移动

图1-1

用相同质量的球做一个弹簧振子和一个单摆，它们运动的周期相同，均为T₀.若均换用质量较大(仍相同)的球，设弹簧振子的周期变为T₁，单摆的周期变为T₂，则有

A．T1＞T2,T2＞T0	B．T1＜T0,T2＜T0
C．T1=T0,T2=T0	D．T1＞T0,T2=T0

如图1-7所示，光滑的半球壳半径为R，O点在球心的正下方，一小球由距O点很近的A点由静止放开，同时在O点正上方有一小球自由落下.若运动中阻力不计，为使两球在O点相碰，小球由多高处自由落下(R)?

图1-7

如图1-6所示，摆长为L的单摆，当摆球由A经平衡位置O向右运动的瞬间，另一小球B以速度v同时通过平衡位置向右运动，B与水平面无摩擦，与竖直墙壁碰撞无能量损失.问OC间距离x满足什么条件，才能使B返回时与A球相遇？

图1-6

将在地球上校准的摆钟拿到月球上去，若此钟在月球记录的时间是1 h，那么实际的时间应是______________h(月球表面的重力加速度是地球表面的1/6).若要把此摆钟调准，应使摆长L₀调节为______________.