高中物理探究单摆的周期与摆长的关系填空题

在地球表面上周期准确的秒摆（周期为2秒），移到距离地面为nR₀的高度处（R₀为地球半径），该秒摆的周期    秒，此时为了让秒摆保持周期2秒不变，则需要    (“增长”，“减短”）摆长．

两个摆长相同的单摆，摆球质量之比是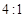，在不同地域振动，当甲摆振动4次的同时，乙摆恰振动5次，则甲、乙二摆所在地区重力加速度之比为        。

一振动周期为T，振幅为A，位于x=0点的波源从平衡位置沿y轴正向开始做简谐振动，该波源产生的一维简谐横波沿x轴正向传播，波速为v，传播过程中无能量损失，一段时间后，该振动传播至某质点P，关于质点P振动的说法正确的是______。（填正确答案标号，选对1个得2分，选对2个得4分，选对3个得5分。每选错1个扣3分，最低得分为0分）

A．振幅一定为A

B．周期一定为T

C．速度的最大值一定为v

D．开始振动的方向沿y轴向上

E．开始振动的方向沿y轴向上或向下取决于它离波源的距离

（(2分)两个单摆的摆长之比为1∶2．摆球质量之比为4∶5 最大摆角之比为3∶2．它们在同一地点做简简运动，则它们的频率之比为         ，

有一单摆，其回复力F与位移x的关系图线如图所示。若摆球质量为100g，则单摆的摆长为________m，从平衡位置开始振动经过1.5s，摆球通过的路程为_________m。

一个理想单摆，已知周期为T，如果由于某种原因（如移到其他星球），自由落体加速度为原来的1/2，振幅为原来的1/3，摆长为原来的1/4，摆球质量为原来的1/5，则它的周期为    。

已知地球和月球的质量分别为M和m，半径分别为R和r。在地球上和月球上周期相等的单摆摆长之比为________，摆长相等的单摆在地球上和月球上周期之比为________。

（1）一条细线下面挂一小球，让小角度自由摆动，它的振动图像如图所示。根据数据估算出它的摆长为________m，摆动的最大偏角正弦值约为________。

（2）一等腰直角三棱镜的截面如图所示，设底边长为4a，一细束光线从AC边的中点P沿平行底边AB方向射入棱镜后，经AB面反射后从BC边的Q点平行入射光线射出，已知Q点到底边的距离为0.5a，求该棱镜的折射率。

某实验小组在利用单摆测定当地重力加速度的实验中：
（1）用游标卡尺测定摆球的直径，测量结果如图所示，则该摆球的直径为________cm.

（2）小组成员在实验过程中有如下说法，其中正确的是________．（填选项前的字母）

A．把单摆从平衡位置拉开30°的摆角，并在释放摆球的同时开始计时

B．测量摆球通过最低点100次的时间t，则单摆周期为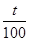

C．用悬线的长度加摆球的直径作为摆长，代入单摆周期公式计算得到的重力加速度值偏大

D．选择密度较小的摆球，测得的重力加速度值误差较小

两个摆长相同的单摆，摆球质量之比是4:1，在不同地域振动，当甲摆振动4次的同时，乙摆恰振动5次，则甲、乙二摆所在地区重力加速度之比为            。

在做“探究单摆周期与摆长的关系”的实验时，用游标卡尺测量摆球直径如图右所示；让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如下图所示，

（1）那么摆球直径为          mm
（2）单摆摆长是         m（保留四位有效数字）
（3）如果测定了若干次全振动的时间如下图中秒表所示，那么秒表读数是______s．

（4）某同学用该实验装置测当地重力加速度，若他测得的g值偏大，可能的原因是（  ）

A．测摆线长时摆线拉得过紧

B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了

C．开始计时时，秒表过迟按下

D．实验中误将50次全振动数为49次

（5）为提高实验精度，在实验中可改变几次摆长L并测出相应的周期T，从而得出一组对应的L与T的数据，再以L为横坐标、T²为纵坐标将所得数据拟合成直线，并求得该直线的斜率K。则重力加速度g =       。(用K及常数表示)

利用单摆测定重力加速度的实验中，已知摆线的长度为l₀，摆球的直径为d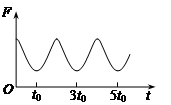

实验时用拉力传感器测得摆线的拉力F随时间t变化的图象如图所示，则单摆的周期
T＝_____；重力加速度的表达式g＝________（用题目中的物理量表示）。

如图，在：半径为2.5m的光滑圆环上切下一小段圆弧，放置于竖直平面内，两端点距最低点高度差H为1cm。将小环置于圆弧端点并从静止释放，小环运动到最低点所需的最短时间为＿＿＿＿s，在最低点处的加速度为＿＿＿＿m/s²。(取g＝10m/s²)

利用单摆测定重力加速度的实验中，已知摆线的长度为l₀，摆球的直径为d

实验时用拉力传感器测得摆线的拉力F随时间t变化的图象如图所示，则单摆的周期
T＝_____；重力加速度的表达式g＝________（用题目中的物理量表示）。

（共4分）某同学在做“利用单摆测重力加速度”实验中，为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l与T的数据，再以l为横坐标、T²为纵坐标将所得数据连成直线，并求得该直线的斜率k。则重力加速度g=       。（用k表示）