高中物理探究单摆的周期与摆长的关系填空题

有两个同学分别在大庆和广州的物理实验室，各自在那里利用先进的DIS系统较准确地探究了“单摆的周期T与摆长l的关系”，他们通过互联网交换实验数据，并由计算机绘制了T²－l图像，如图甲所示．在大庆的同学所测实验结果对应的图线是________(填“A”或“B”)．另外，在广州做探究的同学还利用计算机绘制了a、b两个摆球的振动图像(如图乙)，由图可知，两单摆摆长之比＝________.在t＝1 s时，b球振动的方向是________．

甲　　　　　　　　　          乙

如图，在半径为的光滑圆环上切下一小段圆弧，放置于竖直平面内，两端点距最低点高度差为。将小环置于圆弧端点并从静止释放，小环运动到最低点所需的最短时间为，在最低点处的加速度为。(取)

利用单摆测量某地的重力加速度，现测得摆球质量为m，摆长为L，通过传感器测出摆球运动时位移随时间变化的规律为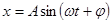，则该单摆的振动周期为       ，该处的重力加速度g=         ；若减小振幅A，则周期       （选填“增大”、“减小”或“不变”）．

如图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置。设摆球向右运动为正方向。图乙是这个单摆的振动图象。(取g＝10 m/s²)

(1)由图象可知，单摆振动的频率为____     ____Hz。
(2)t＝0时，摆球应在___      _____点。
(3)此摆的摆长为___       _____m。

有两个单摆做简谐运动，位移与时间关系是：x₁=3asin(4πbt+)和x₂=9asin(8πbt+)，其中a、b为正的常数，则它们的：振幅之比为__________；摆长之比为_________。

某同学在用单摆测定重力加速度的实验中，测量不同摆长情况下单摆的振动周期，并以L为横坐标，为纵坐标，做出了图线，如图所示，由此图线可知重力加速度为            m/s²。　　　　　　　　　　　　　　　　　　　

一个单摆的振动周期是2s，求下列作简谐运动情况下单摆的周期：
（1）摆长缩短为原来的1/4，单摆的周期为________s；
（2）摆球的质量减为原来的1/4，单摆的周期为________s；
（3）振幅减为原来的1/4，单摆的周期为________s。

两个摆长相同的单摆，摆球质量之比是4:1，在不同地域振动，当甲摆振动4次的同时，乙摆恰振动5次，则甲、乙二摆所在地区重力加速度之比为             。

如图所示的实线和虚线分别表示同一个单摆在A、B两个星球半径大小相同的星球表面上的振动图象，其中实线是A星球上的，虚线是B星球上的，那么两个星球的平均密度ρ_A和ρ_B之比是__________。

如右图甲所示，有一质量为m、带电量为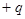的小球在竖直平面内做单摆，摆长为L，当地的重力加速度为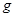，则周期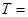        ；若在悬点处放一带正电的小球（图乙），则周期将        。（填“变大”、“不变”、“变小”）

如图所示，半径是0.2m的圆弧状光滑轨道置于竖直面内并固定在地面上，轨道的最低点为B，在轨道的A点（弧AB所对圆心角小于5°）和弧形轨道的圆心O两处各有一个静止的小球Ⅰ和Ⅱ，若将它们同时无初速释放，先到达B点的是________球

将一单摆装置竖直悬挂于某一深度为h（未知）且开口向下的小筒中（单摆的下部分露于筒外），如图(甲)所示，将悬线拉离平衡位置一个小角度后由静止释放，设单摆振动过程中悬线不会碰到筒壁，如果本实验的长度测量工具只能测量出筒的下端口到摆球球心之距l，并通过改变l而测出对应的摆动周期T，再以T²为纵轴、l为横轴做出函数关系图象，就可以通过此图象得出小筒的深度h和当地的重力加速度。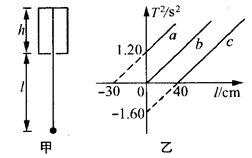

(1)如果实验中所得到的T²—l关系图象如图(乙)所示，那么该同学所画出的图象应该是a、b、c中的________________；
(2)由图象可知，小筒的深度h ＝________m；当地g＝_____________m / s²。

如图所示,为同一个单摆分别在地球和月球上做受迫振动的共振曲线,则图线__________表示的是在地球上单摆的共振曲线,可以求得该单摆的摆长为__________m,月球表面的重力加速度约为__________ m/s².

已知地面重力加速度大约是月面重力加速度的6倍。那么一台地面上的秒摆（运动周期为2.0秒）在月面上的运动周期约为     秒。（结果保留两位有效数字）

在做《用单摆测定重力加速度》的实验时，用摆长l和周期T计算重力加速度的公式是g=           。