高中数学多面角及多面角的性质试题

给出下列命题：
（1）存在实数，使sincos=1；（2）存在实数，使sin+cos=； （3）y=sin（－2x）是偶函数；（4）x=是函数y= sin（2x+）的一条对称轴的方程；（5）若、是第一象限角，且，则sinsin；其中所有的正确命题的序号是      ．

已知函数f（x）=1－cosx，则f（0）+f（1）+f（2）+…+f（20010）=         ．

函数f（x）=的最小正周期和最大值分别为           ．

关于函数f（x）=sin²x－（）^|x|+，有下面四个结论，其中正确结论的个数为（   ）
①f（x）是奇函数；                ②当x＞2009时，f（x）＞恒成立；
③f（x）的最大值是；            ④f（x）的最小值是－；

A．1个

B．2个

C．3个

D．4个

将函数y=sinx－cosx的图象沿x轴向右平移a个单位长度（a0），所得图象关于y轴对称，则a的最小值为                                                   （   ）

A．

B．

C．

D．

函数y=sin（2x+）+2的图象按向量平移得到函数y=sin2x的图象，则向量可以是（   ）

A．（，－2）

B．（－，－2）

C．（－，－2）

D．（，－2）

设A、B、C是ABC的三个内角，且tanA、tanB是方程=0的两个实数根，则ABC是                        （   ）
A．等边三角形    B．等腰直角三角形C．锐角三角形     D．钝角三角形

函数f（x）=cos2x+ sin（x+）是               （   ）

A．非偶非奇函数	B．仅有最小值的奇函数
C．仅有最大值的偶函数	D．既有最小值又有最大值的偶函数

如图，函数y=2sin（x+）（其中xR，0）
的图象与y轴交于点（0，1）． （1）求的值； （2）设P是图象
上的最高点，M、N是图象与x轴的交点，求与的夹角．

已知函数．

（1）求函数的最小正周期和最小值；
（2）在给出的直角坐标系中，用描点法画出函数在区间上的图像．

函数f(x)＝A·tan(ωx+φ)(φ＞0)在区间[m，n]上的函数值都小于0，则函数g(x)＝A·cot(ωx+φ)在[m，n]上的函数值

A．都大于0，且有最大值为g(m)	B．都小于0，且有最大值为g(m)
C．都大于0，且有最小值为g(m)	D．都小于0，且有最小值为g(m)

设，下列命题：①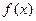既不是奇函数，又不是偶函数；②若是三角形内角，则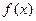是增函数；③若是三角形内角，则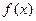有最大值，无最小值； ④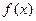的最小正周期为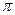，其中正确命题的序号是    (    )

A．①②

B．①③

C．②③

D．②④

已知函数的部分图象如图所示.(Ⅰ) 求函数的解析式；
(Ⅱ) 如何由函数的图象通过适当的变换得到函数的图象, 写出变换过程.

已知函数（其中）的图象与x轴在原点右侧的第一个交点为N（6，0），又
（1）求这个函数解析式
（2）设关于x的方程在[0，8]内有两个不同根，求的值及k的取值范围。

（1）解关于x的不等式
（2）记a>0时（1）中不等式的解集为A，集合B=，若恰有3个元素，求a的取值范围。