给出下列命题:
(1)存在实数 ,使sin
,使sin cos
cos =1;(2)存在实数
=1;(2)存在实数 ,使sin
,使sin +cos
+cos =
=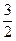 ; (3)y=sin(
; (3)y=sin(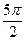 -2x)是偶函数;(4)x=
-2x)是偶函数;(4)x=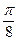 是函数y=
是函数y=  sin(2x+
sin(2x+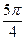 )的一条对称轴的方程;(5)若
)的一条对称轴的方程;(5)若 、
、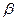 是第一象限角,且
是第一象限角,且
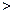
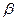 ,则sin
,则sin
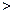 sin
sin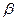 ;其中所有的正确命题的序号是 .
;其中所有的正确命题的序号是 .
相关知识点
推荐套卷
给出下列命题:
(1)存在实数 ,使sin
,使sin cos
cos =1;(2)存在实数
=1;(2)存在实数 ,使sin
,使sin +cos
+cos =
=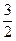 ; (3)y=sin(
; (3)y=sin(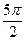 -2x)是偶函数;(4)x=
-2x)是偶函数;(4)x=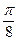 是函数y=
是函数y=  sin(2x+
sin(2x+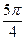 )的一条对称轴的方程;(5)若
)的一条对称轴的方程;(5)若 、
、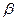 是第一象限角,且
是第一象限角,且
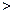
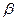 ,则sin
,则sin
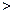 sin
sin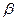 ;其中所有的正确命题的序号是 .
;其中所有的正确命题的序号是 .