如图,在由边长为 个单位长度的小正方形组成的网格中,点 均为格点(网格线的交点).
(1)画出线段 关于直线 对称的线段 ;
(2)将线段 向左平移 个单位长度,再向上平移 个单位长度,得到线段 ,画出线段 ;
(3)描出线段 上的点 及直线 上的点 ,使得直线 垂直平分 .
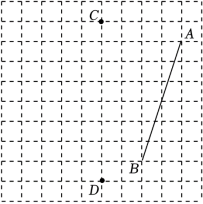
如图,在由边长为 个单位长度的小正方形组成的网格中,点 均为格点(网格线的交点).
(1)画出线段 关于直线 对称的线段 ;
(2)将线段 向左平移 个单位长度,再向上平移 个单位长度,得到线段 ,画出线段 ;
(3)描出线段 上的点 及直线 上的点 ,使得直线 垂直平分 .
