已知: .
求作: ,使
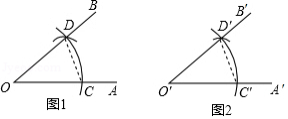
(1)如图1,以点 为圆心,任意长为半径画弧,分别交 , 于点 、 ;
(2)如图2,画一条射线 ,以点 为圆心, 长为半径画弧,交 于点 ;
(3)以点 为圆心, 长为半径画弧,与第2步中所画的弧交于点 ;
(4)过点 画射线 ,则 .
根据以上作图步骤,请你证明 .
相关知识点
推荐套卷
已知: .
求作: ,使
(1)如图1,以点 为圆心,任意长为半径画弧,分别交 , 于点 、 ;
(2)如图2,画一条射线 ,以点 为圆心, 长为半径画弧,交 于点 ;
(3)以点 为圆心, 长为半径画弧,与第2步中所画的弧交于点 ;
(4)过点 画射线 ,则 .
根据以上作图步骤,请你证明 .
