探究:小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点 , , , ,可通过构造直角三角形利用图1得到结论: 他还利用图2证明了线段 的中点 的坐标公式: , .

(1)请你帮小明写出中点坐标公式的证明过程;
运用:(2)①已知点 , ,则线段 长度为 ;
②直接写出以点 , , , 为顶点的平行四边形顶点 的坐标: ;
拓展:(3)如图3,点 在函数 的图象 与 轴正半轴夹角的平分线上,请在 、 轴上分别找出点 、 ,使 的周长最小,简要叙述作图方法,并求出周长的最小值.
相关知识点
推荐套卷
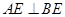 ,垂足为E.
,垂足为E.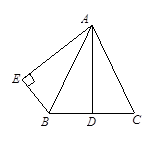 则∠BAC=2∠BAE,请说明理由.
则∠BAC=2∠BAE,请说明理由.
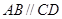 ,
,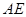 平分
平分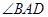 ,
,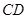 与
与 ,
,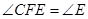 。试说明:
。试说明: 。
。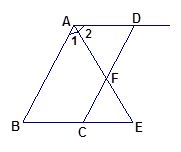
 ,
,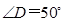 ,求
,求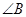 的度数。
的度数。 粤公网安备 44130202000953号
粤公网安备 44130202000953号