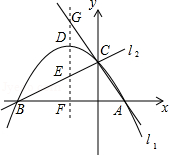
如图,已知两直线 , 分别经过点 ,点 ,且两条直线相交于 轴的正半轴上的点 ,当点 的坐标为 时,恰好有 ,经过点 、 、 的抛物线的对称轴与 、 、 轴分别交于点 、 、 , 为抛物线的顶点.
(1)求抛物线的函数解析式;
(2)试说明 与 的数量关系?并说明理由;
(3)若直线 绕点 旋转时,与抛物线的另一个交点为 ,当 为等腰三角形时,请直接写出点 的坐标.
相关知识点
推荐套卷
如图,已知两直线 , 分别经过点 ,点 ,且两条直线相交于 轴的正半轴上的点 ,当点 的坐标为 时,恰好有 ,经过点 、 、 的抛物线的对称轴与 、 、 轴分别交于点 、 、 , 为抛物线的顶点.
(1)求抛物线的函数解析式;
(2)试说明 与 的数量关系?并说明理由;
(3)若直线 绕点 旋转时,与抛物线的另一个交点为 ,当 为等腰三角形时,请直接写出点 的坐标.
