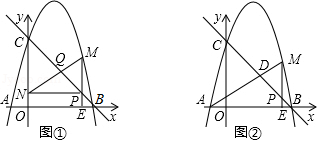
如图，直线 与 轴交于点 ，与 轴交于点 ，抛物线 经过 ， 两点，与 轴另一交点为 ．点 以每秒 个单位长度的速度在线段 上由点 向点 运动（点 不与点 和点 重合），设运动时间为 秒，过点 作 轴垂线交 轴于点 ，交抛物线于点 ．
（1）求抛物线的解析式；
（2）如图①，过点 作 轴垂线交 轴于点 ，连接 交 于点 ，当 时，求 的值；
（3）如图②，连接 交 于点 ，当 是等腰三角形时，直接写出 的值．
（本小题满分8分）如图1，OA、OB是⊙O的半径，且OA⊥OB，点C是OB延长线上任意一点，
过点C作CD切⊙O于点D，连结AD交DC于点E．
（1）求证：CD=CE；
（2）如图2，若将图1中的半径OB所在直线向上平移，交OA于F，交⊙O于B′，其他条件不变，
求证：∠C=2∠A；
（3）如图3，在（2）的条件下，若CD=6．5，AE=3，sinA=
，求⊙O半径OA的长．
（本小题满分8分）如图，A（2，1）是矩形OCBD的对角线OB上的一点，点E在BC上，双曲线ｙ＝
经过点A，交BC于点E，交BD于点F，若CE＝
．
（1）求双曲线的解析式；
（2）求点F的坐标；
（3）连接EF、DC，求证：EF∥DC．
（本小题满分6分）小王购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示．
根据图中的数据（单位：m），解答下列问题：
（1）用含x、y的代数式表示地面总面积；
（2）小王发现客厅面积比卫生间面积大21m2，且地面总面积是卫生间面积的15倍．若铺1m2地砖的平均费用为80元，那么铺地砖的总费用为多少元？
（本小题满分6分）如上图，在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠ECD＝90°，AB与CE交于F，ED与AB、BC分别交于M、H．
（1）求证:CF＝CH；
（2）如下图，△ABC不动，将△EDC绕点C旋转到∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．
粤公网安备 44130202000953号