为了增强学生的环保意识，某校组织了一次全校2000名学生都参加的“环保知识”考试，考题共10题．考试结束后，学校团委随机抽查部分考生的考卷，对考生答题情况进行分析统计，发现所抽查的考卷中答对题量最少为6题，并且绘制了如下两幅不完整的统计图．请根据统计图提供的信息解答以下问题：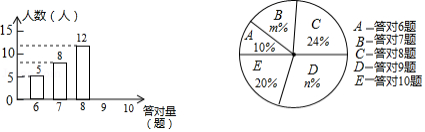
（1）本次抽查的样本容量是 ；在扇形统计图中， ， ，“答对8题”所对应扇形的圆心角为 度；
（2）将条形统计图补充完整；
（3）请根据以上调查结果，估算出该校答对不少于8题的学生人数．
相关试题
如图 (1) 地图中由街道构成的两个三角形全等吗？如果全等请给图形作上恰当的字母标记 ，并说明两个三角形全等的理由。 (2) 如果你站在中山路和南京路的交叉口，你想去动物园
走哪一条路线最近？请简要说明理由。
一个不透明的布袋中装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同。
(1) 摸一个球，记下颜色后放回，并拌匀，在摸出一个球，求两次摸出的球颜色恰好不同的概率（要求用树状图或列表法说明）。
(2) 再将n个白球放入袋中，拌匀，使摸出一个球是白球的概率是
，求n的值。
聪明的你试试看吧！
（1）分析图①，②，④中阴影部分的分布规律，按此规律在图③中画出其中的阴影部分。
（2）在下列的图形上补一个小正方形，使它成为一个轴对称图形。
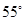, ∠AEP=
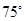, 求△ABC的各个内角的度数。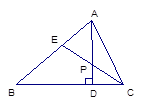
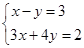（2）
相关知识点
推荐套卷
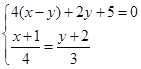
粤公网安备 44130202000953号