垃圾的分类回收不仅能够减少环境污染、美化家园,甚至能够变废为宝、节约资源.为增强学生垃圾分类意识,推动垃圾分类进校园,某中学组织全校1565名学生参加了“垃圾分类知识竞赛”(满分为100分).该校数学兴趣小组为了解全校学生竞赛分数情况,采用简单随机抽样的方法(即每名学生的竞赛分数被抽到的可能性相等的抽样方法)抽取部分学生的竞赛分数进行调查分析.
(1)以下三种抽样调查方案:
方案一:从七年级、八年级、九年级中指定部分学生的竞赛分数作为样本;
方案二:从七年级、八年级中随机抽取部分男生的竞赛分数以及在九年级中随机抽取部分女生的竞赛分数作为样本;
方案三:从全校1565名学生的竞赛分数中随机抽取部分学生的竞赛分数作为样本.
其中抽取的样本最具有代表性和广泛性的一种抽样调查方案是 (填写“方案一”、“方案二”或“方案三” ;
(2)该校数学兴趣小组根据简单随机抽样方法获得的样本,绘制出如下统计表 分及以上为“优秀”,60分及以上为“及格”,学生竞赛分数记为 分)
|
样本容量 |
平均分 |
及格率 |
优秀率 |
最高分 |
最低分 |
|
100 |
83.59 |
|
|
100 |
52 |
|
分数段 |
|
|
|
|
|
|
频数 |
5 |
7 |
18 |
30 |
40 |
结合上述信息解答下列问题:
①样本数据的中位数所在分数段为 ;
②全校1565名学生,估计竞赛分数达到“优秀”的学生有 人.
为了弘扬爱国主义精神,某校组织了"共和国成就"知识竞赛,将成绩分为: (优秀)、 (良好)、 (合格)、 (不合格)四个等级.小李随机调查了部分同学的竞赛成绩,绘制了如图统计图.
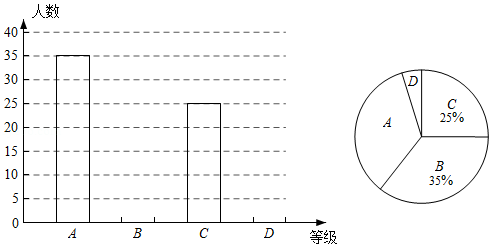
(1)本次抽样调查的样本容量是 ,请补全条形统计图;
(2)已知调查对象中只有两位女生竞赛成绩不合格,小李准备随机回访两位竞赛成绩不合格的同学,请用树状图或列表法求出恰好回访到一男一女的概率;
(3)该校共有2000名学生,请你估计该校竞赛成绩"优秀"的学生人数.
为庆祝中国共产党成立100周年,在中小学生心中厚植爱党情怀,我市开展“童心向党”教育实践活动,某校准备组织学生参加唱歌,舞蹈,书法,国学诵读活动,为了解学生的参与情况,该校随机抽取了部分学生进行“你愿意参加哪一项活动”(必选且只选一种)的问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)这次抽样调查的总人数为 人,扇形统计图中“舞蹈”对应的圆心角度数为 ;
(2)若该校有1400名学生,估计选择参加书法的有多少人?
(3)学校准备从推荐的4位同学(两男两女)中选取2人主持活动,根据画树状图或表格法求恰为一男一女的概率.

为了保护环境加强环保教育,某中学组织学生参加义务收集废旧电池的活动,下面是随机抽取40名学生对收集废旧电池的数量进行的统计:
|
废旧电池数 节 |
4 |
5 |
6 |
7 |
8 |
|
人数 人 |
9 |
11 |
11 |
5 |
4 |
请根据学生收集到的废旧电池数,判断下列说法正确的是
| A. |
样本为40名学生 |
B. |
众数是11节 |
| C. |
中位数是6节 |
D. |
平均数是5.6节 |
五一期间,某地相关部门对观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整),根据图中的信息,下列结论错误的是
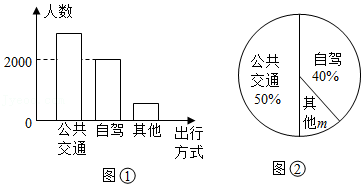
| A. |
本次抽样调查的样本容量是5000 |
| B. |
扇形统计图中的 为 |
| C. |
若五一期间观光的游客有50万人,则选择自驾方式出行的大约有20万人 |
| D. |
样本中选择公共交通出行的有2400人 |
为推进扬州市"青少年茁壮成长工程",某校开展"每日健身操"活动,为了解学生对"每日健身操"活动的喜欢程度,随机抽取了部分学生进行调查,将调查信息结果绘制成如下尚不完整的统计图表:

抽样调查各类喜欢程度人数统计表
|
喜欢程度 |
人数 |
|
.非常喜欢 |
50人 |
|
.比较喜欢 |
人 |
|
.无所谓 |
人 |
|
.不喜欢 |
16人 |
根据以上信息,回答下列问题:
(1)本次调查的样本容量是 ;
(2)扇形统计图中表示 程度的扇形圆心角为 ,统计表中 ;
(3)根据抽样调查的结果,请你估计该校2000名学生中大约有多少名学生喜欢"每日健身操"活动(包含非常喜欢和比较喜欢).
为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据"厨余垃圾"、"有害垃圾"、"可回收物"和"其他垃圾"这四类标准将垃圾分类处理.调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制成统计图.
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)已知该小区有居民2000人,请估计该小区对垃圾分类知识"完全了解"的居民人数.
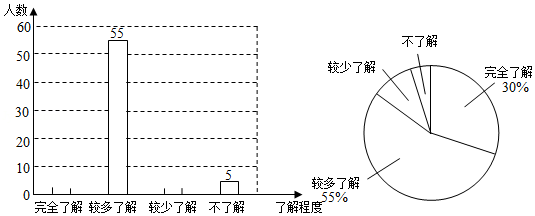
某校有4000名学生,随机抽取了400名学生进行体重调查,下列说法错误的是
| A. |
总体是该校4000名学生的体重 |
| B. |
个体是每一个学生 |
| C. |
样本是抽取的400名学生的体重 |
| D. |
样本容量是400 |
为了解落实国家《关于全面加强新时代大中小学劳动教育的意见》的实施情况,某校从全体学生中随机抽取部分学生,调查他们平均每周劳动时间 (单位: ,按劳动时间分为四组: 组“ ”, 组“ ”, 组“ ”, 组“ ”.将收集的数据整理后,绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)这次抽样调查的样本容量是 , 组所在扇形的圆心角的大小是 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请你估计该校平均每周劳动时间不少于 的学生人数.
近些年来,移动支付已成为人们的主要支付方式之一.某企业为了解员工某月 , 两种移动支付方式的使用情况,从企业2000名员工中随机抽取了200人,发现样本中 , 两种支付方式都不使用的有10人,样本中仅使用 种支付方式和仅使用 种支付方式的员工支付金额 (元 分布情况如表:
|
支付金额 (元 |
|
|
|
|
仅使用 |
36人 |
18人 |
6人 |
|
仅使用 |
20人 |
28人 |
2人 |
下面有四个推断:
①根据样本数据估计,企业2000名员工中,同时使用 , 两种支付方式的为800人;
②本次调查抽取的样本容量为200人;
③样本中仅使用 种支付方式的员工,该月支付金额的中位数一定不超过1000元;
④样本中仅使用 种支付方式的员工,该月支付金额的众数一定为1500元.
其中正确的是
| A. |
①③ |
B. |
③④ |
C. |
①② |
D. |
②④ |
某校为了了解本校学生每天课后进行体育锻炼的时间情况,在5月份某天随机抽取了若干名学生进行调查,调查发现学生每天课后进行体育锻炼的时间都不超过100分钟,现将调查结果绘制成两幅尚不完整的统计图表.请根据统计图表提供的信息,解答下列问题:
|
组别 |
锻炼时间(分 |
频数(人) |
百分比 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
6 |
|
|
|
|
3 |
|
(1)本次调查的样本容量是 ;表中 , ;
(2)将频数分布直方图补充完整;
(3)已知 组有2名男生和1名女生,从中随机抽取两名学生,恰好抽到1名男生和1名女生的概率是 ;
(4)若该校学生共有2200人,请根据以上调查结果估计:该校每天课后进行体育锻炼的时间超过60分钟的学生共有多少人?
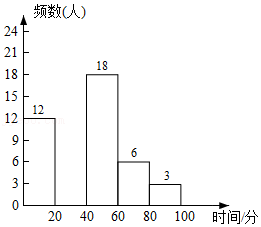
为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对初二级部学生进行了问卷调查,其中一项是:疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图(不完整)如图.由图中信息可知,下列结论错误的是

A.本次调查的样本容量是600
B.选“责任”的有120人
C.扇形统计图中“生命”所对应的扇形圆心角度数为
D.选“感恩”的人数最多
为了提高学生的综合素养,某校开设了五门手工活动课,按照类别分为: "剪纸"、 "沙画"、 "葫芦雕刻"、 "泥塑"、 "插花".为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如图两幅不完整的统计图.

根据以上信息,回答下列问题:
(1)本次调查的样本容量为 ;统计图中的 , ;
(2)通过计算补全条形统计图;
(3)该校共有2500名学生,请你估计全校喜爱"葫芦雕刻"的学生人数.
江苏省第十九届运动会将于2018年9月在扬州举行开幕式,某校为了了解学生“最喜爱的省运会项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表
|
最喜爱的项目 |
人数 |
|
篮球 |
20 |
|
羽毛球 |
9 |
|
自行车 |
10 |
|
游泳 |
|
|
其他 |
|
|
合计 |
根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 , .
(2)扇形统计图中“自行车”对应的扇形的圆心角为 .
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
