为了解落实国家《关于全面加强新时代大中小学劳动教育的意见》的实施情况,某校从全体学生中随机抽取部分学生,调查他们平均每周劳动时间 (单位: ,按劳动时间分为四组: 组“ ”, 组“ ”, 组“ ”, 组“ ”.将收集的数据整理后,绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)这次抽样调查的样本容量是 , 组所在扇形的圆心角的大小是 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请你估计该校平均每周劳动时间不少于 的学生人数.
相关知识点
推荐套卷
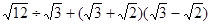
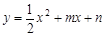 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.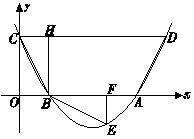
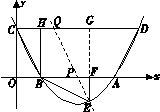
 .请根据图中信息,解答下列问题:
.请根据图中信息,解答下列问题: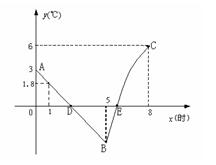

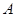 、
、 、
、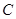 是⊙O上的三点,
是⊙O上的三点, .
. 平分
平分 .
. 作
作 于点
于点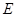 ,交
,交 . 若
. 若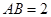 ,
,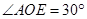 ,求
,求 的长. )
的长. )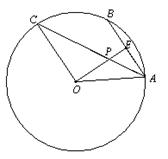
 粤公网安备 44130202000953号
粤公网安备 44130202000953号