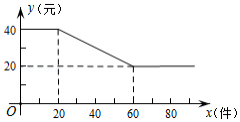
某工厂生产一种火爆的网红电子产品，每件产品成本16元、工厂将该产品进行网络批发，批发单价 （元 与一次性批发量 （件 为正整数）之间满足如图所示的函数关系．
（1）直接写出 与 之间所满足的函数关系式，并写出自变量 的取值范围；
（2）若一次性批发量不超过60件，当批发量为多少件时，工厂获利最大？最大利润是多少？
4月20日8时2分，四川省雅安市芦山县发生了7.0级地震，当地的部分房屋严重受损，上万灾民无家可归，灾情牵动亿万中国人的心。某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地，若用大、小两种货车共20辆，恰好能一次性运完这批物资。已知这两种货车的载重量分别为16吨/辆和10吨/辆，运往甲、乙两地的运费如下表：
| 车 型 运往地 |
甲 地（元/辆） |
乙 地（元/辆） |
| 大货车 |
720 |
800 |
| 小货车 |
500 |
650 |
（1）求这两种货车各用多少辆？
（2）如果安排9辆货车前往甲地，其余货车前往乙地，设前往甲地的大货车为
辆，前往甲、乙两地的总运费为w元，求出w与的函数关系式（写出自变量的取值范围）；
（3）在（2）的条件下，若运往甲地的物资不少于132吨，请你设计出使总运费最少的货车调配方案，并求出最少总运费
如图，在矩形纸片ABCD中，AB=3，BC=4．把△BCD沿对角线BD折叠，使点C落在E处，BE交AD于点F；
（1）求证：AF＝EF；
（2）求tan∠ABF的值；
（3）连接AC交BE于点G,求AG的长．
如图，点P是菱形ABCD对角线BD上一点，连接CP并延长交AD于点E，交BA的延长线于点F.
(1)求证：∠DCP＝∠DAP；
（2）若AB=2，DP∶PB＝1∶2，且PA⊥BF,求对角线BD的长.
如图，已知A(-4,n)，B(1,-4)是一次函数
的图象和反比例函数
的图象的两个交点．
(1)求反比例函数和一次函数的解析式；
(2)求直线
与
轴的交点
的坐标及△
的面积；
(3)求不等式
的解集（请直接写出答案）.
粤公网安备 44130202000953号