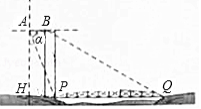
如图示一架水平飞行的无人机 的尾端点 测得正前方的桥的左端点 的
俯角为 其中 ,无人机的飞行高度 为 米,桥的长度为1255米.
①求点 到桥左端点 的距离;
②若无人机前端点 测得正前方的桥的右端点 的俯角为 ,求这架无人机的长度 .
相关知识点
推荐套卷
如图示一架水平飞行的无人机 的尾端点 测得正前方的桥的左端点 的
俯角为 其中 ,无人机的飞行高度 为 米,桥的长度为1255米.
①求点 到桥左端点 的距离;
②若无人机前端点 测得正前方的桥的右端点 的俯角为 ,求这架无人机的长度 .
