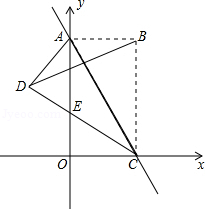
如图， 在平面直角坐标系中， 把矩形 沿对角线 所在直线折叠， 点 落在点 处， 与 轴相交于点 ，矩形 的边 ， 的长是关于 的一元二次方程 的两个根， 且 ．
（1） 求线段 ， 的长；
（2） 求证： ，并求出线段 的长；
（3） 直接写出点 的坐标；
（4） 若 是直线 上一个动点， 在坐标平面内是否存在点 ，使以点 ， ， ， 为顶点的四边形是菱形？若存在， 请直接写出 点的坐标；若不存在， 请说明理由 ．
相关试题
如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．
学习“一次函数”时，我们从“数”和“形”两方面研究一次函数的性质，并积累了一些经验和方法，尝试用你积累的经验和方法解决下面问题．
（1）在平面直角坐标系中，画出函数y=|x|的图象：
①列表：完成表格
| x |
… |
﹣3 |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
… |
| y |
… |
②画出y=|x|的图象；
（2）结合所画函数图象，写出y=|x|两条不同类型的性质；
（3）直接写出函数y=|x﹣2|图象是由函数y=|x|图象怎样平移得到？
已知：图中点A，点B的坐标分别为（﹣2，1）和（2，3）．
（1）在图（1）中分别画出线段AB关于x轴和y轴的对称线段A1B1及A2B2；
（2）在图（2）中分别画出线段AB关于直线x=﹣1和直线y=4的对称线段A3B3及A4B4；
（3）写出点A3、B3与点A4、B4的坐标．
相关知识点
推荐套卷
粤公网安备 44130202000953号