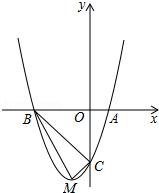
如图，顶点为 的抛物线 分别与 轴相交于点 ， （点 在点 的右侧），与 轴相交于点 ．
（1）求抛物线的函数表达式；
（2）判断 是否为直角三角形，并说明理由．
（3）抛物线上是否存在点 （点 与点 不重合），使得以点 ， ， ， 为顶点的四边形的面积与四边形 的面积相等？若存在，求出点 的坐标；若不存在，请说明理由．
相关试题
如图，已知抛物线y＝ax2＋bx＋4与x轴交于A（－2,0）、B两点，与y轴交于C点，其对称轴为直线x＝1.
（1）直接写出抛物线的解析式：
（2）把线段AC沿x轴向右平移，设平移后A、C的对应点分别为A′、C′，当C′落在抛物线上时，求A′、C′的坐标；
（3）除（2）中的点A′、C′外，在x轴和抛物线上是否还分别存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形，若存在，求出E、F的坐标；若不存在，请说明理由.
某公司经营一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：w＝－2x＋240.设这种绿茶在这段时间的销售利润为y（元），解答下列问题：
（1）求y与x的关系式
（2）当x取何值时，销售利润最大？最大利润是多少？
，其中x是方程
的根.据媒体报道，我国2010年公民出境旅游总人数约5000万人次，2012年公民出境旅游总人数约7200万人次，若2011年、2012年公民出境旅游总人数逐年递增，请解答下列问题：
（1）求这两年我国公民出境旅游总人数的年平均增长率；
（2）如果2012年仍保持相同的年平均增长率，请你预测2013年我国公民出境旅游总人数约多少万人次？
相关知识点
推荐套卷
粤公网安备 44130202000953号