(1)【探究发现】
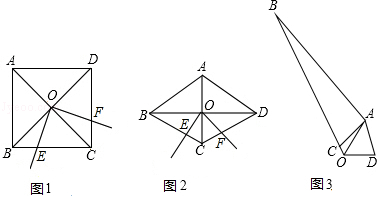
如图1,∠ EOF的顶点 O在正方形 ABCD两条对角线的交点处,∠ EOF=90°,将∠ EOF绕点 O旋转,旋转过程中,∠ EOF的两边分别与正方形 ABCD的边 BC和 CD交于点 E和点 F(点 F与点 C, D不重合).则 CE, CF, BC之间满足的数量关系是 .
(2)【类比应用】
如图2,若将(1)中的"正方形 ABCD"改为"∠ BCD=120°的菱形 ABCD",其他条件不变,当∠ EOF=60°时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)【拓展延伸】
如图3,∠ BOD=120°, OD= , OB=4, OA平分∠ BOD, AB= ,且 OB>2 OA,点 C是 OB上一点,∠ CAD=60°,求 OC的长.
推荐套卷


 如果AB : AC="AC" : BC,那么称点C为线段
如果AB : AC="AC" : BC,那么称点C为线段 的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线
的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线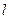 将一个面积为S的图形分成两部分,这两部分的面积分别为S1: S2,如果S : S1= S1: S2,,那么称直线
将一个面积为S的图形分成两部分,这两部分的面积分别为S1: S2,如果S : S1= S1: S2,,那么称直线 中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?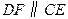 ,交 AC于点F,连接EF(如图3),则直线EF是△ABC的黄金分割线.请说明理由.
,交 AC于点F,连接EF(如图3),则直线EF是△ABC的黄金分割线.请说明理由. ABCD的边AB的黄金分割点,过点E作
ABCD的边AB的黄金分割点,过点E作 ,交DC于点F,显然直线EF是
,交DC于点F,显然直线EF是 ABCD的黄金分割线,使它不经过
ABCD的黄金分割线,使它不经过



 粤公网安备 44130202000953号
粤公网安备 44130202000953号