扬州教育推出的"智慧学堂"已成为同学们课外学习的得力助手．为了解同学们"智慧学堂"平台使用的熟练程度，某校随机抽取了部分同学进行调查，并将调查结果绘制成如图两幅尚不完整的统计图．
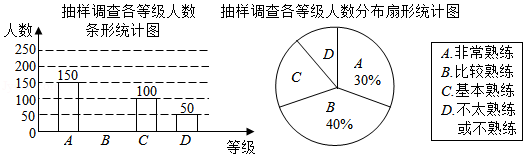
根据以上信息，回答下列问题：
（1）本次调查的样本容量是 ，扇形统计图中表示 等级的扇形圆心角为 ；
（2）补全条形统计图；
（3）学校拟对"不太熟练或不熟练"的同学进行平台使用的培训，若该校有2000名学生，试估计该校需要培训的学生人数．
相关试题
≌△CAD；
中，
，
垂足为E，
垂足为D，
cm，
cm，求
的长．
如图：在平面直角坐标系中A(-1,5),B(-1,0)C(-4,3).
(1)求出△ABC的面积；
(2)在下图中作出△ABC关于y轴对称图形△A1B1C1；
(3)写出A1 、B1 、C1的坐标。
相关知识点
推荐套卷
粤公网安备 44130202000953号