中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.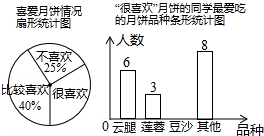
(注
参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为
度;
条形统计图中,喜欢“豆沙”月饼的学生有 人;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”月饼的共有 人.
(3)甲同学最爱吃云腿月饼,乙同学最爱吃豆沙月饼,现有重量、包装完全一样的云腿、豆沙、莲蓉、蛋黄四种月饼各一个,让甲、乙每人各选一个,请用画树状图法或列表法,求出甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率.