已知圆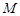 :
: ,设点
,设点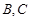 是直线
是直线 :
: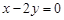 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点
,点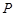 在线段
在线段 上,过
上,过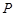 点作圆
点作圆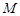 的切线
的切线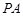 ,切点为
,切点为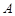 .
.
(1)若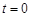 ,
,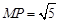 ,求直线
,求直线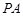 的方程;
的方程;
(2)若O为原点,经过 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 长的最小值
长的最小值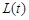 .
.
相关知识点
推荐套卷
已知圆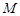 :
: ,设点
,设点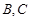 是直线
是直线 :
: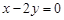 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点
,点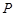 在线段
在线段 上,过
上,过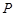 点作圆
点作圆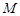 的切线
的切线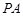 ,切点为
,切点为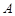 .
.
(1)若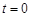 ,
,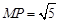 ,求直线
,求直线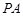 的方程;
的方程;
(2)若O为原点,经过 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 长的最小值
长的最小值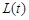 .
.