如图，直线l：y=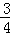
x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．
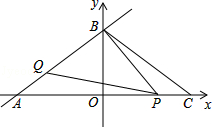
（1）点A坐标是 ，点B的坐标 ，BC= ．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．
，其中x=﹣1．
；
；
≤
相关知识点
推荐套卷
如图，直线l：y=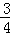x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．
（1）点A坐标是 ，点B的坐标 ，BC= ．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．
粤公网安备 44130202000953号