某市海产品市场管理部门规划建造面积为2400平方米的集贸大棚,大棚内设A种类型和B种类型的店面共80间,每间A种类型的店面的平均面积为28平方米,月租费为400元;每间B种类型的店面的平均面积为20平方米,月租费为360元.全部店面的建造面积不低于大棚总面积的80%,又不能超过大棚总面积的85℅.试确定A种类型店面的数量的范围;
该大棚管理部门通过了解业主的租赁意向得知,A种类型店面的出租率为75%,B种类型店面的出租率为90%,为使店面的月租费最高,最高月租金是多少?
相关知识点
推荐套卷
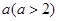 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.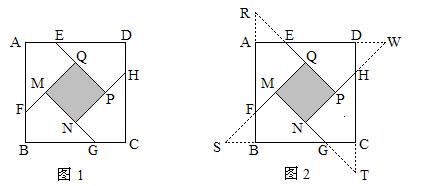
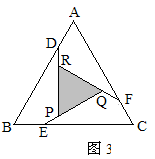
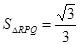 ,则AD的长为__________.
,则AD的长为__________. (
(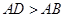 ),将纸片折叠一次,使点
),将纸片折叠一次,使点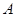 与
与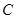 重合,再展开,折痕
重合,再展开,折痕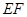 交
交 边于
边于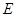 ,交
,交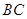 边于
边于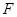 ,AC与EF交于点O,分别连结
,AC与EF交于点O,分别连结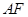 和
和 .在线段
.在线段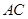 上是否存在一点
上是否存在一点 ,使得2AE2=AC·AP?若存在,请说明点
,使得2AE2=AC·AP?若存在,请说明点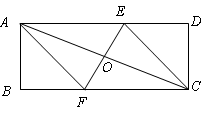


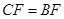 ;
;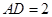 ,⊙O的半径为3,求BC的长.
,⊙O的半径为3,求BC的长. ,
, 表示),请你根据下面的示意图,求电车每隔几分钟(用t表示)从车站开出一部?
表示),请你根据下面的示意图,求电车每隔几分钟(用t表示)从车站开出一部?
 粤公网安备 44130202000953号
粤公网安备 44130202000953号