已知关于 的一元二次方程x2-4x+k+1=0
的一元二次方程x2-4x+k+1=0
(1)若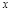 =-1是方程的一个根,求k值和方程的另一根;
=-1是方程的一个根,求k值和方程的另一根;
(2)设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根,是否存在实数k,使得x1x2>x1+x2成立?请说明理由.
相关知识点
推荐套卷
已知关于 的一元二次方程x2-4x+k+1=0
的一元二次方程x2-4x+k+1=0
(1)若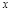 =-1是方程的一个根,求k值和方程的另一根;
=-1是方程的一个根,求k值和方程的另一根;
(2)设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根,是否存在实数k,使得x1x2>x1+x2成立?请说明理由.