为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天睡眠时间,设每名学生的平均每天睡眠时间为 时,共分为四组: . , . , . , . ,将调查结果绘制成如图两幅不完整的统计图:
注:学生的平均每天睡眠时间不低于6时且不高于10时.

请回答下列问题:
(1)本次共调查了 名学生;
(2)请补全频数分布直方图;
(3)求扇形统计图中 组所对应的圆心角度数;
(4)若该校有1500名学生,根据抽样调查结果,请估计该校有多少名学生平均每天睡眠时间低于7时.
相关知识点
推荐套卷
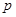 万元援助灾区
万元援助灾区 所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第
所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第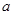 都是正整数)
都是正整数)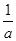
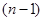 所学校
所学校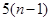
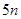
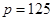 时,该企业能援助多少所学校?
时,该企业能援助多少所学校? 万元的捐款,按照原来的分配方案援助其它学校.若
万元的捐款,按照原来的分配方案援助其它学校.若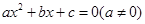 中,如果
中,如果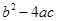 ≥
≥ ,那么它的两个实数根是
,那么它的两个实数根是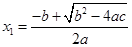 ,
,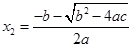 .
.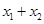 、
、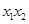 的值(用含
的值(用含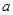 、
、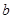 、
、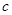 的代数式表示);
的代数式表示);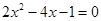 的两个根分别为
的两个根分别为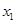 、
、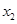 ,根据(1)所求的结果,不解方程,直接写出
,根据(1)所求的结果,不解方程,直接写出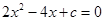 的一根是
的一根是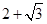 ,请你利用(1)中根与系数的关系求出方程的另一根及
,请你利用(1)中根与系数的关系求出方程的另一根及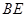 平分
平分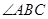 ,交
,交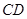 于点
于点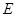 ,点
,点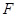 在边
在边 上.
上.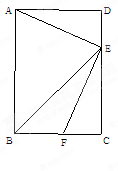
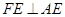 ,那么
,那么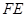 和
和 相等吗?证明你的结论
相等吗?证明你的结论 .
.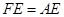 ,那么
,那么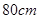 的绳子剪成两段,并把每一段绳子围成一个正方形.
的绳子剪成两段,并把每一段绳子围成一个正方形.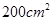 ,该怎么剪?
,该怎么剪?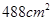 吗?
吗?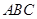 中,
中,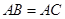 ,
,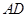 、
、 分別是△
分別是△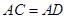 ;
;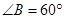 ,试说明四边形
,试说明四边形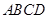 是菱形.
是菱形.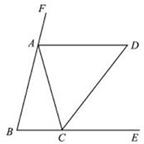
 粤公网安备 44130202000953号
粤公网安备 44130202000953号