已知关于 的一元二次函数
的一元二次函数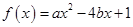 .
.
(1)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为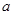 和
和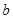 ,求函数
,求函数 在区间
在区间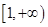 上是增函数的概率;
上是增函数的概率;
(2)设点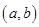 是区域
是区域 内的随机点,求函数
内的随机点,求函数 上是增函数的概率.
上是增函数的概率.
相关知识点
推荐套卷
已知关于 的一元二次函数
的一元二次函数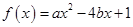 .
.
(1)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为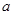 和
和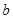 ,求函数
,求函数 在区间
在区间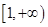 上是增函数的概率;
上是增函数的概率;
(2)设点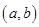 是区域
是区域 内的随机点,求函数
内的随机点,求函数 上是增函数的概率.
上是增函数的概率.