在某社区举办的《有奖知识问答比赛》中,甲、乙、丙三人同时回答某一道题,已知甲回答对这道题的概率是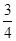 ,甲、丙二人都回答错的概率是
,甲、丙二人都回答错的概率是 ,乙、丙二人都回答对的概率是
,乙、丙二人都回答对的概率是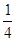 .
.
(Ⅰ)求乙、丙二人各自回答对这道题的概率;
(Ⅱ)设乙、丙二人中回答对该题的人数为X,求X的分布列和数学期望.
推荐套卷
在某社区举办的《有奖知识问答比赛》中,甲、乙、丙三人同时回答某一道题,已知甲回答对这道题的概率是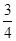 ,甲、丙二人都回答错的概率是
,甲、丙二人都回答错的概率是 ,乙、丙二人都回答对的概率是
,乙、丙二人都回答对的概率是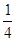 .
.
(Ⅰ)求乙、丙二人各自回答对这道题的概率;
(Ⅱ)设乙、丙二人中回答对该题的人数为X,求X的分布列和数学期望.