眉山市三苏雕像广场是为了纪念三苏父子而修建的．原是一块长为
米，宽为
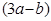米的长方形地块，现在政府对广场进行改造，计划将如图四周阴影部分进行绿化，中间将保留边长为
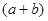米的正方形三苏父子雕像，则绿化的面积是多少平方米？并求出当
时的绿化面积．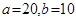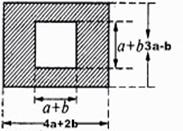
相关试题
，求
的值。
即
， 所以
，求
的值。
、
的代数式表示地面总面积；推荐套卷
眉山市三苏雕像广场是为了纪念三苏父子而修建的．原是一块长为米，宽为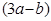米的长方形地块，现在政府对广场进行改造，计划将如图四周阴影部分进行绿化，中间将保留边长为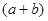米的正方形三苏父子雕像，则绿化的面积是多少平方米？并求出当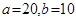时的绿化面积．
粤公网安备 44130202000953号